题目内容

已知矩形ABCD，AB=4，BC=3，沿对角线AC将矩形ABCD折成一个空间四边形，则空间四边形ABCD的外接球的体积为


  1. A.
    数学公式π
  2. B.
    数学公式π
  3. C.
    数学公式π
  4. D.
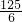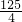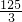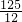    数学公式π
A
分析：先确定球心的位置，然后求出球的半径，再解出外接球的体积
解答：由题意知，球心到四个顶点的距离相等，
所以球心为对角线AC的中点，且其半径为AC长度的一半，
则V球=π×（）3=．
故选 A
点评：本题考查球的内接多面体，球的体积，考查学生发现问题解决问题的能力，是基础题．
练习册系列答案
相关题目
精英家教网已知矩形ABCD中，AB=2
2
，BC=1．以AB的中点O为原点建立如图所示的平面直角坐标系xoy．
（1）求以A，B为焦点，且过C，D两点的椭圆的标准方程；
（2）过点P（0，2）的直线l与（1）中的椭圆交于M，N两点，是否存在直线l，使得以线段MN为直径的圆恰好过原点？若存在，求出直线l的方程；若不存在，说明理由．
已知矩形ABCD的顶点都在半径为5的球O的球面上，且AB=6，BC=2
5
，则棱锥O-ABCD的侧面积为（　　）
如图所示，已知矩形ABCD中，AB=
2
，AD=1，将△ABD沿BD折起，使点A在平面BCD内的射影落在DC上．
（1）求证：平面ADC⊥平面BCD；
（2）求点C到平面ABD的距离；
（3）若E为BD中点，求二面角B-AD-C的大小．
如图,已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB,交SB于E,过E作EF⊥SC交SC于F.

(1)求证:AF⊥SC;

(2)若平面AEF交SD于G,求证:AG⊥SD.

已知矩形ABCD中,A(-4,4)、D(5,7),中心E在第一象限内且与y轴的距离为一个单位,动点P(x,y)沿矩形一边BC运动,求的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网