题目内容
(本小题14分)在数列 中,
中, =0,且对任意k
=0,且对任意k ,
, 成等差数列,其公差为2k. (Ⅰ)证明
成等差数列,其公差为2k. (Ⅰ)证明 成等比数列;
成等比数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)记 . 证明: 当
. 证明: 当 为偶数时, 有
为偶数时, 有 .
.
解:(I)(5分)证明:由题设可知, ,
, ,
, ,
, ,
, 。从而
。从而 ,所以
,所以 ,
, ,
, 成等比数列。
成等比数列。
(II)(5分)解:由题设可得
所以

 .
.
由 ,得
,得 ,从而
,从而 .
.
所以数列 的通项公式为
的通项公式为 或写为
或写为 ,
, 。
。
(III)(4分)证明:由(II)可知 当 为偶数时,
为偶数时, ;
;
当 为奇数时,
为奇数时, .
.
易知 时,
时, . 不等式成立。
. 不等式成立。
又当 为偶数且
为偶数且 时,
时,





 ,从而
,从而 ,不等式也成立。
,不等式也成立。
综上,当 为偶数时,有
为偶数时,有 .
.
解析

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
(本小题14分)在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛。
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为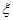 (
(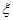 所有取值为0,1,2,3...,10)分别为
所有取值为0,1,2,3...,10)分别为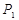 、
、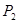 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0 |
0 |
0 |
0 |
0.06 |
0.04 |
0.06 |
0.3 |
0.2 |
0.3 |
0.04 |
|
|
0 |
0 |
0 |
0 |
0.04 |
|
0.05 |
0.2 |
0.32 |
0.32 |
0.02 |
① 若1,2号运动员各射箭一次,求两人中至少有一人命中9环的概率;
② ②判断1号,2号射箭运动员谁射箭的水平高?并说明理由.
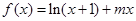 ,当
,当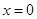 时,函数
时,函数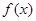 取得极大值.
取得极大值.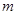 的值;(Ⅱ)已知结论:若函数
的值;(Ⅱ)已知结论:若函数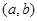 内导数都存在,且
内导数都存在,且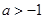 ,则存在
,则存在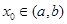 ,使得
,使得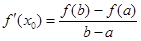 .试用这个结论证明:若
.试用这个结论证明:若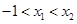 ,函数
,函数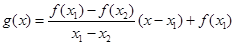 ,则对任意
,则对任意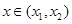 ,都有
,都有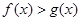 ;(Ⅲ)已知正数
;(Ⅲ)已知正数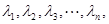 满足
满足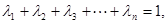 求证:当
求证:当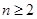 ,
,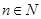 时,对任意大于
时,对任意大于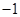 ,且互不相等的实数
,且互不相等的实数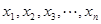 ,都有
,都有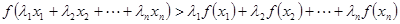
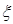
 0.05
0.05