题目内容
化简:sin2α•sin2β+cos2α•cos2β-
cos2α•cos2β=( )
| 1 |
| 2 |
分析:把原式的最后一项利用二倍角的余弦函数公式化简,并把化简的式子提取
,合并后利用同角三角函数间的基本关系化简后,即可得到值.
| 1 |
| 2 |
解答:解:∵cos2αcos2β=(cos2α-sin2α)(cos2β-sin2β)
=cos2αcos2β-cos2αsin2β-sin2αcos2β+sin2αsin2β,
∴sin2α•sin2β+cos2α•cos2β-
cos2α•cos2β
=
(2sin2α•sin2β+2cos2α•cos2β-cos2αcos2β+cos2αsin2β+sin2αcos2β-sin2αsin2β)
=
(sin2αsin2β+cos2αcos2β+cos2αsin2β+sin2αcos2β)
=
[sin2β(sin2α+cos2α)+cos2β(sin2α+cos2α)]
=
(sin2β+cos2β)
=
.
故选B
=cos2αcos2β-cos2αsin2β-sin2αcos2β+sin2αsin2β,
∴sin2α•sin2β+cos2α•cos2β-
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
故选B
点评:此题考查了三角函数的化简求值,涉及的知识有二倍角的余弦函数公式,以及同角三角函数间的基本关系,熟练掌握公式及基本关系是解本题的关键.

练习册系列答案
相关题目
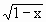 ,化简f(sin2θ)+f[sin(-2θ)],其中0<θ<π.
,化简f(sin2θ)+f[sin(-2θ)],其中0<θ<π. 得
得