题目内容
已知椭圆方程为
（1）写出椭圆的顶点坐标和焦点坐标．
（2）若等轴双曲线C与该椭圆有相同焦点，求双曲线标准方程．
解：（1）椭圆方程为，所以a=4，b=2
，c=2；所以顶点
，焦点（±2，0）
（2）由于双曲线的焦点坐标为（2，0），所以双曲线的方程为：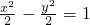
．
分析：（1）利用椭圆的方程直接求出a，b，c即可得到顶点坐标，焦点坐标．
（2）求出等轴双曲线的焦点坐标，即可求出双曲线的方程．
点评：本题是基础题，考查椭圆的方程的应用，基本性质的应用，等轴双曲线的定义，考查计算能力．
，所以a=4，b=2，c=2；所以顶点，焦点（±2，0）（2）由于双曲线的焦点坐标为（2，0），所以双曲线的方程为：
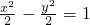．分析：（1）利用椭圆的方程直接求出a，b，c即可得到顶点坐标，焦点坐标．
（2）求出等轴双曲线的焦点坐标，即可求出双曲线的方程．
点评：本题是基础题，考查椭圆的方程的应用，基本性质的应用，等轴双曲线的定义，考查计算能力．
练习册系列答案
相关题目
=1，射线y=2
x（x≥0）与椭圆的交点为M，过M作倾斜角互补的两条直线，分别与椭圆交于A、B两点（异于M）．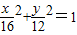
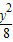=1，射线y=2
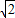x（x≥0）与椭圆的交点为M，过M作倾斜角互补的两条直线，分别与椭圆交于A、B两点（异于M）．
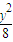=1，射线y=2
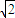x（x≥0）与椭圆的交点为M，过M作倾斜角互补的两条直线，分别与椭圆交于A、B两点（异于M）．