题目内容
已知椭圆方程为x2+ =1,射线y=2
=1,射线y=2 x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(1)求证直线AB的斜率为定值;
(2)求△AMB面积的最大值.
解:(1)∵斜率k存在,不妨设k>0,求出M( ,2),
,2),
直线MA方程为y-2=k(x- ),直线MB方程为y-2=-k(x-
),直线MB方程为y-2=-k(x- ).
).
分别与椭圆方程联立,可解出xA= -
- ,xB=
,xB= -
- .
.
则yA=2-k(x- ),yB=2+k(x-
),yB=2+k(x- ),
),
kAB= =2
=2 ;
;
∴kAB=2 (定值).
(定值).
(2)设直线AB方程为y=2 x+m,与x2+
x+m,与x2+ =1联立,消去y得16x2+4
=1联立,消去y得16x2+4 mx+(m2-8)=0
mx+(m2-8)=0
由△>0得-4<m<4,且m≠0,点M到AB的距离d= .
.
设△AMB的面积为S.∴S2= |AB|2d2=
|AB|2d2= m2(16-m2)≤
m2(16-m2)≤ •
• =2.
=2.
当m=±2 时,得Smax=
时,得Smax= .
.
分析:(1)设k>0,求得M的坐标,则可表示出AM的直线方程和BM的直线方程,分别与椭圆的方程联立求得xA和xB,进而求得AB的斜率.
(2)设出直线AB的方程与椭圆方程联立消去y,利用判别式大于0求得m的范围,进而表示出三角形AMB的面积,利用m的范围确定面积的最大值.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题和解决问题的能力.
 ,2),
,2),直线MA方程为y-2=k(x-
 ),直线MB方程为y-2=-k(x-
),直线MB方程为y-2=-k(x- ).
).分别与椭圆方程联立,可解出xA=
 -
- ,xB=
,xB= -
- .
.则yA=2-k(x-
 ),yB=2+k(x-
),yB=2+k(x- ),
),kAB=
 =2
=2 ;
;∴kAB=2
 (定值).
(定值).(2)设直线AB方程为y=2
 x+m,与x2+
x+m,与x2+ =1联立,消去y得16x2+4
=1联立,消去y得16x2+4 mx+(m2-8)=0
mx+(m2-8)=0由△>0得-4<m<4,且m≠0,点M到AB的距离d=
 .
.设△AMB的面积为S.∴S2=
 |AB|2d2=
|AB|2d2= m2(16-m2)≤
m2(16-m2)≤ •
• =2.
=2.当m=±2
 时,得Smax=
时,得Smax= .
.分析:(1)设k>0,求得M的坐标,则可表示出AM的直线方程和BM的直线方程,分别与椭圆的方程联立求得xA和xB,进而求得AB的斜率.
(2)设出直线AB的方程与椭圆方程联立消去y,利用判别式大于0求得m的范围,进而表示出三角形AMB的面积,利用m的范围确定面积的最大值.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了学生分析问题和解决问题的能力.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
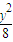 =1,射线y=2
=1,射线y=2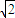 x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M). =1,射线y=2
=1,射线y=2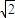 x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
x(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).