题目内容
已知函数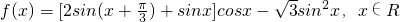
(I)求函数f(x)的最小正周期;
(II)求f(x)在 上的最大值和最小值.
上的最大值和最小值.
解:因为
=[2(sinxcos +sin
+sin cosx)+sinx]cosx-
cosx)+sinx]cosx-
=sin2x+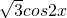
= 于是
于是
(I)函数f(x)的最小正周期T= .
.
(II) ∴
∴
∴ 即:1≤y≤2
即:1≤y≤2
∴f(x)max=2,f(x)min=1
分析:(I)利用两角和的正弦函数,化简函数的表达式,利用二倍角公式、两角和的正弦函数化为一个角的一个三角函数的形式,直接利用周期公式求函数f(x)I的最小正周期;
(II)根据 求出
求出 ,然后求出函数的最大值和最小值.
,然后求出函数的最大值和最小值.
点评:本题是基础题,考查三角函数的化简求值,周期的应用,最值的求法,考查计算能力.

=[2(sinxcos
 +sin
+sin cosx)+sinx]cosx-
cosx)+sinx]cosx-
=sin2x+
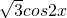
=
 于是
于是(I)函数f(x)的最小正周期T=
 .
.(II)
 ∴
∴
∴
 即:1≤y≤2
即:1≤y≤2∴f(x)max=2,f(x)min=1
分析:(I)利用两角和的正弦函数,化简函数的表达式,利用二倍角公式、两角和的正弦函数化为一个角的一个三角函数的形式,直接利用周期公式求函数f(x)I的最小正周期;
(II)根据
 求出
求出 ,然后求出函数的最大值和最小值.
,然后求出函数的最大值和最小值.点评:本题是基础题,考查三角函数的化简求值,周期的应用,最值的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
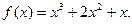
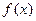 的单调区间与极值;
的单调区间与极值;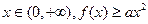 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。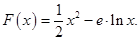
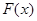 的最小值;
的最小值; 和
和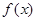 定义域内的任意实数
定义域内的任意实数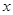 ,若存在常数
,若存在常数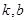 ,使得不等式
,使得不等式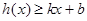 和
和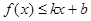 都成立,则称直线
都成立,则称直线 是函数
是函数 ,
,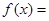
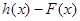 ,试问函数
,试问函数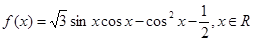
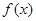 的最小值和最小正周期;
的最小值和最小正周期;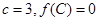 ,若向量
,若向量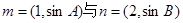 共线,求a,b的值。
共线,求a,b的值。