题目内容
1.已知f(x)是定义在R上的偶函数,当x>0时,f(x)=$\left\{\begin{array}{l}{ax+lo{g}_{5}x,}&{x>4}\\{{x}^{2}+{2}^{x}+3,}&{0<x≤4}\end{array}\right.$,若f(-5)<f(2),则a的取值范围为( )| A. | (-∞,1) | B. | (-∞,2) | C. | (-2,+∞) | D. | (2,+∞) |
分析 由已知当x<0时,f(x)=$\left\{\begin{array}{l}{-ax+lo{g}_{5}(-x),x<-4}\\{{x}^{2}+{2}^{-x}+3,-4≤x<0}\end{array}\right.$,从而f(-5)=5a+1,f(2)=11,由此利用f(-5)<f(2),能求出a的取值范围.
解答 解:∵f(x)是定义在R上的偶函数,当x>0时,f(x)=$\left\{\begin{array}{l}{ax+lo{g}_{5}x,}&{x>4}\\{{x}^{2}+{2}^{x}+3,}&{0<x≤4}\end{array}\right.$,
∴当x<0时,f(x)=$\left\{\begin{array}{l}{-ax+lo{g}_{5}(-x),x<-4}\\{{x}^{2}+{2}^{-x}+3,-4≤x<0}\end{array}\right.$,
∴f(-5)=5a+1,f(2)=4+4+3=11,
∵f(-5)<f(2),
∴5a+1<11,解得a<2.
∴a的取值范围为(-∞,2).
故选:B.
点评 本题考查实数取值范围的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
12.在直角△ABC中,AD为斜边BC边上的高,则下列结论错误的是( )
| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
16. 如图是一个四棱锥的三视图,则该几何体的体积为( )
如图是一个四棱锥的三视图,则该几何体的体积为( )
 如图是一个四棱锥的三视图,则该几何体的体积为( )
如图是一个四棱锥的三视图,则该几何体的体积为( )| A. | 8 | B. | 9 | C. | 12 | D. | 16 |
12.设复数z1=-1+2i,z2=2+i,其中i为虚数单位,则z1•z2=( )
| A. | -4 | B. | 3i | C. | -3+4i | D. | -4+3i |
8.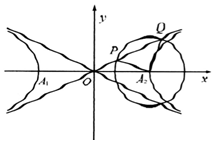 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
 如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )
如图,已知过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点A2作一个圆,该圆与其渐近线bx-ay=0交于点P,Q,若∠PA2Q=90°,|PQ|=2|OP|,则该双曲线的离心率为( )| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{3}$ |
 ,则
,则 的值为 ( )
的值为 ( ) B.
B. C.
C. D.
D.