Question

已知函数f(x)的图像与函数h(x)＝x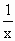＋＋2的图像关于点A(0，1)对称．

(1)求f(x)的解析式；

(2)(文)若g(x)＝f(x)·x＋ax，且g(x)在区间(0，2]上为减函数，求实数a的取值范围；

(理)若g(x)＝f(x)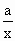＋，且g(x)在区间(0，2]上为减函数，求实数a的取值范围．

Answer 1

答案：
解析：

解：(1)设f(x)图像上任一点坐标为(x，y)，点(x，y)关于点A(0，1)的对称点(－x，2－y)在h(x)图像上 　　∴2－y＝－x＋＋2，∴y＝x＋，即f(x)＝x＋ 　　(2)文：g(x)＝(x＋)·x＋ax，即g(x)＝x2＋ax＋1 　　g(x)在(0，2]上递减－≥2，∴a≤－4 　　理：g(x)＝x＋，∵(x)＝1－ 　　g(x)在(0，2]上递减，∴1－≤0在x∈(0，2]时恒成立． 　　即a≥x2－1在x∈(0，2]时恒成立． 　　∵x∈(0，2]时，(x2－1)max＝3　　∴a≥3