题目内容
已知曲线x2+2y2+4x+4y+4=0按向量a=(2,1)平移后得到曲线C.
(1)求曲线C的方程;
(2)过点D(0,2)的直线与曲线C相交于不同的两点M、N,且M在D、N之间,设 ,求实数λ的取值范围.
,求实数λ的取值范围.
(1)求曲线C的方程;
(2)过点D(0,2)的直线与曲线C相交于不同的两点M、N,且M在D、N之间,设
 ,求实数λ的取值范围.
,求实数λ的取值范围.[ ,+∞)
,+∞)
 ,+∞)
,+∞)(1)原曲线即为(x+2)2+2(y+1)2=2,则平移后的曲线C为x2+2y2=2,
即 +y2=1.
+y2=1.
(2)设M(x1,y1),N(x2,y2),则
 由于点M、N在椭圆x2+2y2=2上,则
由于点M、N在椭圆x2+2y2=2上,则
即 ,消去x22得,2λ2+8λy2+8=2λ2+4λ+2,即y2=
,消去x22得,2λ2+8λy2+8=2λ2+4λ+2,即y2= .
.
∵-1≤y2≤1,∴-1≤ ≤1.又∵λ>0,故解得λ≥
≤1.又∵λ>0,故解得λ≥ .
.
故λ的取值范围为[ ,+∞).
,+∞).
即
 +y2=1.
+y2=1.(2)设M(x1,y1),N(x2,y2),则
 由于点M、N在椭圆x2+2y2=2上,则
由于点M、N在椭圆x2+2y2=2上,则
即
 ,消去x22得,2λ2+8λy2+8=2λ2+4λ+2,即y2=
,消去x22得,2λ2+8λy2+8=2λ2+4λ+2,即y2= .
.∵-1≤y2≤1,∴-1≤
 ≤1.又∵λ>0,故解得λ≥
≤1.又∵λ>0,故解得λ≥ .
.故λ的取值范围为[
 ,+∞).
,+∞).
练习册系列答案
相关题目
 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
. ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离 的最小值.
的最小值.




 ,则此直线的斜率是( ).
,则此直线的斜率是( ).

 的倾斜角为 .
的倾斜角为 . 的焦点
的焦点 作倾角为
作倾角为 的直线,与抛物线分别交于
的直线,与抛物线分别交于 、
、 两点(
两点(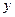 轴左侧),则
轴左侧),则 。
。