题目内容
19.定义函数:G(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{1,x<0}\end{array}\right.$,下列结论正确的②③①G(a)G(b)=G(a+b);
②G(a)+G(b)≥2G($\frac{a+b}{2}$);
③G(a+b)≥1+a+b;
④G(ab)=G(a)G(b)
分析 画出函数G(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{1,x<0}\end{array}\right.$的图象,数形结合逐一分析四个结论的真假,可得答案.
解答 解:G(x)=$\left\{\begin{array}{l}{{e}^{x},x≥0}\\{1,x<0}\end{array}\right.$的图象如下图所示:
当a<0,b>0时,G(a)G(b)=G(a+b)不成立,故①错误;
函数在y轴左侧的图象平等于x轴不具有凸凹性,函数在y轴右侧为凹函数,
故G(a)+G(b)≥2G($\frac{a+b}{2}$)恒成立,故②正确;
由图可得:G(x)≥1+x恒成立,故G(a+b)≥1+a+b恒成立,故③正确;
当a,b>2时,G(ab)=G(a)G(b)不成立,故④错误;
故正确的结论是:②③,
故答案为:②③
点评 本题考查的知识点是分段函数的应用,数形结合思想,难度中档.

练习册系列答案
相关题目
 已知函数f(x)=x|x-m|,x∈R.且f(4)=0
已知函数f(x)=x|x-m|,x∈R.且f(4)=0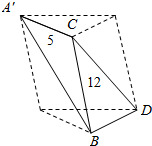 将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.
将两直角边长分别为5和12的直角三角板的一条直角边对接成三棱锥A′-BCD,使A′C与BD成60°角,求体积VA′-BCD.