题目内容
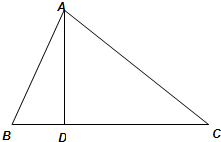
在△ABC中，AD为∠BAC的平分线，求证：| AB |
| AC |
| BD |
| DC |
分析：做出辅助线，过C作CE∥AD，交BA的延长线于E，根据所做的平行，得到对应线段成比例，根据角平分线所分的角相等和两直线平行同位角和内错角相等，得到等腰三角形，等量代换，得到要求证的比例式成立．
解答：
证明：过C作CE∥AD，交BA的延长线于E，如图所示．
∵AD∥CE，∴
=
．
又∵AD平分∠BAC，
∴∠BAD=∠DAC，
在△BCE中，由AD∥CE知，
∠BAD=∠E，∠DAC=∠ACE，
∴∠ACE=∠E，∴AE=AC．
∴
=
=
．
故
=
．
证明：过C作CE∥AD，交BA的延长线于E，如图所示．∵AD∥CE，∴
| BA |
| AE |
| BD |
| DC |
又∵AD平分∠BAC，
∴∠BAD=∠DAC，
在△BCE中，由AD∥CE知，
∠BAD=∠E，∠DAC=∠ACE，
∴∠ACE=∠E，∴AE=AC．
∴
| BD |
| DC |
| AB |
| AE |
| AB |
| AC |
故
| AB |
| AC |
| BD |
| DC |
点评：本题考查平行线分线段成比例定理，考查两条直线平行的性质，考查等量代换，本题是一个基础题，实际上本题是证明的三角形内角平分线定理．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
如图，在△ABC中，AD为BC边上的高，垂足D在边BC上，∠CAD=2∠BAD=2θ（0＜θ＜
已知在△ABC中，AD为∠BAC的平分线，以C为圆心，CD为半径的半圆交BC的延长线于点E，交AD于点F，交AE于点M，且∠B=∠CAE，EF：FD=4：3．
已知：在△ABC中，AD为∠BAC的平分线，AD的垂直平分线EF与AD交于点E，与BC的延长线交于点F，若CF=4，BC=5，则DF=在△ABC中，AD为BC边上的中线，|
|=2|
|=2|
|=4，则|
|=（ ）
| AC |
| AB |
| AD |
| BD |
A、
| ||
| B、2 | ||
C、
| ||
| D、3 |