题目内容
已知平行四边形的两条边所在的直线方程分别是x+y+1=0和3x-y+4=0,它的对角线的交点是M(3,0),求这个四边形的其它两边所在的直线方程.
分析:根据平行四边形的两条边所在的直线方程求出它们所在的直线的斜率,再利用两直线平行的条件得出这个四边形的其它两边所在的直线斜率,结合中点坐标公式求出另两条边的交点,从而求出这个四边形的其它两边所在的直线方程.
解答:解:由
的相邻两条边的交点为(-
,
),
又对角线的交点为M(3,0),
由中点坐标公式得:
另两条边的交点为(2×3-(-
),2×0-
)即(
,-
),
且这两条边所在直线的斜率分别等于直线x+y+1=0和3x-y+4=0的斜率,为-1和3,
由点斜式知,所求两条直线的方程为y+
=-(x-
)和y+
=3(x-
),
即x+y-7=0和3x-y-22=0.
|
| 5 |
| 4 |
| 1 |
| 4 |
又对角线的交点为M(3,0),
由中点坐标公式得:
另两条边的交点为(2×3-(-
| 5 |
| 4 |
| 1 |
| 4 |
| 29 |
| 4 |
| 1 |
| 4 |
且这两条边所在直线的斜率分别等于直线x+y+1=0和3x-y+4=0的斜率,为-1和3,
由点斜式知,所求两条直线的方程为y+
| 1 |
| 4 |
| 29 |
| 4 |
| 1 |
| 4 |
| 29 |
| 4 |
即x+y-7=0和3x-y-22=0.
点评:本小题主要考查两直线平行的条件、直线的一般式方程等基础知识,考查运算求解能力,考查转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
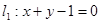 ,
,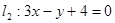 ,
且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
,
且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.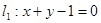 ,
,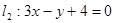 ,
且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.
,
且它的对角线的交点是M(3,3),求这个平行四边形其它两边所在直线的方程.