题目内容
6.已知函数f(n)=sin$\frac{nπ}{6}$(n∈Z),求值:(1)f(1)+f(2)+f(3)+…f(102)
(2)f(1)f(2)f(3)…f(101)
分析 (1)根据函数解析式得出周期为:T=$\frac{2π}{\frac{π}{6}}$=12,f(1)+…+f(12)=0,转化为f(1)+f(2)+f(3)+…f(102)=f(1)+f(2)+…+(6),判断即可.
(2)利用f(6)=0,很容易得出f(1)f(2)f(3)…f(101)=0,
解答 解:(1)∵函数f(n)=sin$\frac{nπ}{6}$(n∈Z),
∴周期为:T=$\frac{2π}{\frac{π}{6}}$=12,
∴f(1)+…+f(12)=0
∴f(1)+f(2)+f(3)+…f(102)=f(1)+f(2)+…+(6)=2+$\sqrt{3}$,
(2)∵f(6)=0,
∴f(1)f(2)f(3)…f(101)=0,
点评 本题考查了三角函数的周期性,利用三角函数的值求解,属于计算题,难度不大.

练习册系列答案
相关题目
17.已知集合A=|x|x>1|,B=|xy=$\sqrt{9-{x}^{2}}$|.那么A∩B=( )
| A. | [-3,3] | B. | (-1,3] | C. | (1,3] | D. | (1,3) |




 ,若
,若 是从
是从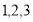 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则使函数
三个数中任取的一个数,则使函数 有极值点的概率为_______.
有极值点的概率为_______.