题目内容
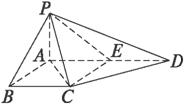
如图四棱锥P-ABCD的底面为正方形,PA⊥平面ABCD,AB=2,PC与平面ABCD成45°角,E、F分别为PA、PB的中点.
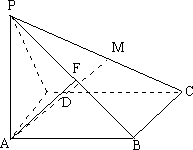
(1)求异面直线DE与AF所成角的大小;
(2)设M是PC上的动点,试问当M在何处时,才能使AM⊥平面PBD,证明你的结论.
解析:
|
解:(1)如图,建立空间直角坐标系,则A(0,0,0),F(1,0, 设 则cos= ∴DE与AF所成的角为arccos (2)∵PA⊥平面ABCD,∴PA⊥BD. 又ABCD是正方形,∴BD⊥AC,BD⊥平面PAC,∴BD⊥AM. 由题意可设M点坐标为(t,t,2 ∴ 设AM⊥PB,∴ ∴t= ∴M在 法二:(1)连CF、EF取CD的中点G,连EG、AG,由题意EF⊥ ∴四边形EDGF为平行四边形,∴FG⊥ED. ∴∠AFG即DE和AF所成的角(或其补角). 又PC与底面所成角45°,∴PA=AC=2 ∴cos∠AFG= ∴连AC交BD于O,AC⊥BD,PA⊥BD. ∴BD⊥平面PAC,∴BD⊥BD. 欲使AM⊥平面PDB,则只需AM⊥PO即可. 在Rt△PAC中,(如图)过C作CH∥PA交AM处长线于H, 又 |
提示:
|
分析:(1).求异面直线所成角一般通过直线平移,或用空间向量. (2)探究性问题考虑当AM⊥平面PBD,M点特点和性质. 说明:本题体现高考立体几何解答题考查的三个热点问题:一是用空间向理求线线角问题;二是线线、线面平行与垂直问题;三是探究性问题. |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 =
=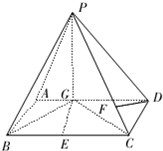 已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且
已知如图四棱锥P-ABCD中,底面ABCD是平行四边形,PG⊥平面ABC,垂足G在AD上,且 ,F是BC的中点.
,F是BC的中点.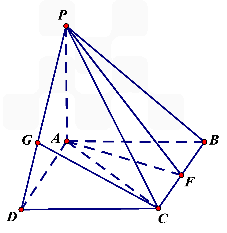
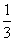 GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.
GD,GB⊥GC,GB=GC=2,PC=4,E是BC的中点.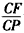 的值。
的值。 
 ,E是BC的中点.
,E是BC的中点. 的值.
的值.