题目内容
已知f（x）是偶函数，它在[0，+∞）上是增函数，若f（lg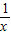
）＞f（1）则x的取值范围是（ ）A．（
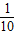，1]B．（0，
）∪（1，+∞）C．（
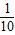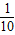，10）D．（0，
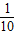）∪（10，+∞）
【答案】分析：根据对数的单调性，我们先解出f（lg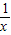
）＞f（1）在[0，+∞）上的解集，再利用偶函数的性质，即可得到满足f（lg
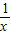）＞f（1）的x的取值范围．
解答：解：在[0，+∞）上
∵f（x）是增函数，
∴f（lg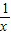
）＞f（1）可化为lg
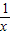＞1
即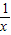
＞10，解得0＜x＜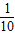
又∵f（x）是偶函数，
∴在（-∞，0）上f（lg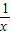
）＞f（1）的解为：-
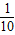＜x＜0
综上，f（lg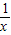
）＞f（1）则x的取值范围是（0，
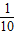）∪（10，+∞）
故选D
点评：本题考查的知识点是奇偶性与单调性的综合，对数函数的单调性与特殊点，熟练掌握函数的性质的性质是解答本题的关键．
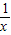）＞f（1）在[0，+∞）上的解集，再利用偶函数的性质，即可得到满足f（lg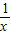）＞f（1）的x的取值范围．解答：解：在[0，+∞）上
∵f（x）是增函数，
∴f（lg
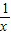）＞f（1）可化为lg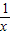＞1即
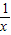＞10，解得0＜x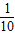＜又∵f（x）是偶函数，
∴在（-∞，0）上f（lg
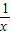）＞f（1）的解为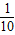：-＜x＜0综上，f（lg
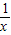）＞f（1）则x的取值范围是（0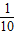，）∪（10，+∞）故选D
点评：本题考查的知识点是奇偶性与单调性的综合，对数函数的单调性与特殊点，熟练掌握函数的性质的性质是解答本题的关键．
练习册系列答案
金博士一点全通系列答案
相关题目
已知f（x）是偶函数，且f（x）在[0，+∞）上是增函数，如果f（ax+1）≤f（x-2）在x∈[
，1]上恒成立，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、[-2，1] |
| B、[-5，0] |
| C、[-5，1] |
| D、[-2，0] |