题目内容
如图2-7，已知在△ABC中，AB=AC，以AB为直径的⊙O交BC于D，过D点作⊙O的切线交AC于E.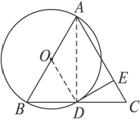
图2-7
求证：（1）DE⊥AC；
（2）BD2=CE·CA.
思路分析:本例是考查切线的性质与直径所对的圆周角是直角的综合题，掌握常见的辅助线作法是解题关键，即连结圆心和切点的半径，根据切线的性质，则有半径垂直于这条切线.
证明:(1)连结OD、AD.
∵DE是⊙O的切线，D为切点，
∴OD⊥DE.
∵AB是⊙O的直径，
∴AD⊥BC.∴AB=AC，BD=DC.
∴OD∥AC，DE⊥AC.
(2)∵AD⊥BC，DE⊥AC，
∴△CDE∽△CAD.
∴
.∴CD2=CE·CA.
∴BD=DC.∴BD2=CE·CA.
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
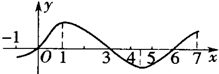设定义在[-1，7]上的函数y=f（x）的图象如图所示．已知（a，b）是
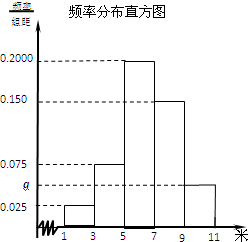为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11）五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
的值及参加“掷铅球”项目测试的人数；
,0)是圆内一点。Q是圆上一动点，AQ的垂直平分线交OQ于P，当点Q在圆C上运动一周时，点P的轨迹为曲线E。
）内变化时，求△AB1B2的面积S(θ)的最大值。