题目内容
【题目】某公司引进一条价值30万元的产品生产线,经过预测和计算,得到生产成本降低![]() 万元与技术改造投入
万元与技术改造投入![]() 万元之间满足:①
万元之间满足:①![]() 与
与![]() 和
和![]() 的乘积成正比;②当
的乘积成正比;②当![]() 时,
时, ![]() ,并且技术改造投入比率
,并且技术改造投入比率![]() ,
, ![]() 为常数且
为常数且![]() .
.
(1)求![]() 的解析式及其定义域;
的解析式及其定义域;
(2)求![]() 的最大值及相应的
的最大值及相应的![]() 值.
值.
【答案】(1)![]() ,定义域是
,定义域是![]() (2)见解析
(2)见解析
【解析】试题分析:(1)先求比例系数,再比率范围得定义域(2)先求导数,再求定义区间上导函数零点,列表分析导函数符号变化规律,确定单调性,进而确定最大值
试题解析:(1)设![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() ,解得
,解得![]() ,
,
所以![]() ,
,
因为![]() ,所以函数的定义域是
,所以函数的定义域是![]() .
.
(2)因为![]() (
(![]() ),
),
所以![]() ,令
,令![]() ,则
,则![]() (舍去)或
(舍去)或![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是增函数,
上是增函数,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上是减函数,
上是减函数,
所以![]() 为函数
为函数![]() 的极大值点,
的极大值点,
当![]() ,即
,即![]() ,
, ![]() ;
;
当![]() ,即
,即![]() 时,
时, 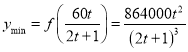 ,
,
综上可得,当![]() 时,
时, ![]() 的最大值为
的最大值为![]() ,
, ![]() 的值为20;
的值为20;
当![]() 时,
时, ![]() 的最大值为
的最大值为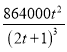 ,
, ![]() 的值为
的值为![]() .
.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目