题目内容
若直线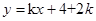 与曲线
与曲线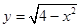 有两个交点,则
有两个交点,则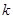 的取值范围是( )
的取值范围是( )
A.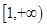 B.
B. 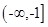 C.
C.
 D.
D.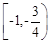
【答案】
D
【解析】
试题分析:由题意可知,作图

曲线 即x2+y2=4,(y≥0)
即x2+y2=4,(y≥0)
表示一个以(0,0)为圆心,以2为半径的位于x轴上方的半圆,如上图所示:
直线y=kx+4+2k即y=k(x+2)+4,表示恒过点(-2,4)斜率为k的直线,结合图形可得,
kAB=-1,∵ =2解得k=-
=2解得k=- 即kAT=-
即kAT=-
∴要使直线与半圆有两个不同的交点,k的取值范围是[-1,- ],故选D
],故选D
考点:本题主要是考查直线与圆的位置关系的运用。
点评:解决该试题的关键是理解直线表示的为过定点(-2,4),斜率为k的直线,而曲线表示的为半个圆,圆心在原点,半径为2的上半个圆,利用数形结合得到结论。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
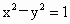 及直线l:y=kx-1.
及直线l:y=kx-1.
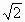 ,求实数k的值.
,求实数k的值.