题目内容
4．若函数y=f′（x）在区间（x1，x2）内是单调递减函数，则函数y=f（x）在区间（x1，x2）内的图象可以是（ ）| A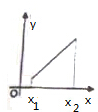． |  | B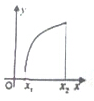． |  | C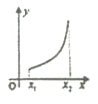． |  | D． |  |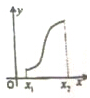
分析 y=f′（x）在区间（x1，x2）内是单调递减函数，则函数的切线斜率越来越小，根据函数切线的斜率变化情况进行讨论即可．
解答 解：y=f′（x）在区间（x1，x2）内是单调递减函数，
则函数的切线斜率越来越小．
A．函数为直线，函数的导数f′（x）=c，不具备单调性，不满足条件．
B．函数的切线斜率越来越小，满足条件．
C．函数的切线斜率越来越大，不满足条件．
D．函数的切线斜率一开始越来越大，然后越来越小，不满足条件．
故选：B
点评 本题主要考查函数的图象的判断，根据导数的几何意义是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
15．若x∈（0，$\frac{π}{2}$），$y∈（0，\frac{π}{2}）$，且tan2x=3tan（x-y），则x+y的可能取值是（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{7π}{12}$ |