题目内容
定义两个平面向量的一种运算
?
=|
|•|
|sin<
,
>,则关于平面向量上述运算的以下结论中,
①
?
=
?
,
②λ(
?
)=(λ
)?
,
③若
=λ
,则
?
=0,
④若
=λ
,且λ>0,则(
+
)?
=(
?
)+(
?
).
恒成立的有( )
| a |
| b |
| a |
| b |
| a |
| b |
①
| a |
| b |
| b |
| a |
②λ(
| a |
| b |
| a |
| b |
③若
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| b |
| c |
| a |
| c |
| b |
| c |
恒成立的有( )
| A.4个 | B.3个 | C.2个 | D.1个 |
①∵
?
=|
| |
|sin<
,
>=
?
,故,故恒成立;
②∵λ(
?
)=λ|
| |
|sin<
,
>,而(λ
)?
=|λ
||
|sin<
,
>,当λ<0时,λ(
?
)=(λ
)?
,不成立;
③若
=λ
,则sin<
,
>=0,得到
?
=0,故恒成立;
④若
=λ
,且λ>0,则
+
=(1+λ)
,
∴(
+
)?
=|(1+λ)||
||
|sin<
,
>,
而(
?
)+(
?
)=|λ
||
|sin<
,
>+|
||
|sin<
,
>=|1+λ||
||
|sin<
,
>.
故(
+
)?
=(
?
)+(
?
)恒成立.
综上可知:只有①③④恒成立.
故选B.
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
②∵λ(
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
③若
| a |
| b |
| a |
| b |
| a |
| b |
④若
| a |
| b |
| a |
| b |
| b |
∴(
| a |
| b |
| c |
| b |
| c |
| b |
| c |
而(
| a |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
| b |
| c |
故(
| a |
| b |
| c |
| a |
| c |
| b |
| c |
综上可知:只有①③④恒成立.
故选B.

练习册系列答案
相关题目
 ,
, ,不妨设向量
,不妨设向量 的方向是向上的,那么向量
的方向是向上的,那么向量 的坐标是(
的坐标是( ).过原点作向量
).过原点作向量 ,则点P的坐标是(
,则点P的坐标是( ),而且直线OP的倾斜角也是α.根据正切函数的定义得
),而且直线OP的倾斜角也是α.根据正切函数的定义得
 ,
,
 ,平行于向量
,平行于向量 的直线方程;
的直线方程;
 的关系;
的关系;
 和
和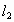 的方程分别是
的方程分别是
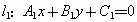

 ∥
∥ ,
, 的条件各是什么?如果它们相交,如何得到它们的夹角公式?
的条件各是什么?如果它们相交,如何得到它们的夹角公式?
 到直线
到直线 的距离公式如何推导?
的距离公式如何推导?

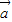 ?
?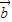 =|
=|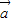 |•|
|•|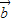 |sin<
|sin<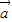 ,
,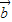 >,则关于平面向量上述运算的以下结论中,
>,则关于平面向量上述运算的以下结论中,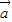 ?
?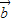 =
=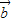 ?
?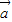 ,
,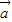 ?
?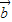 )=(λ
)=(λ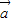 )?
)?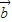 ,
,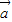 =λ
=λ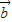 ,则
,则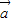 ?
?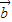 =0,
=0,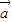 =λ
=λ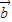 ,且λ>0,则(
,且λ>0,则(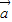 +
+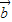 )?
)?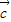 =(
=( ?
?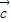 )+(
)+(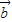 ?
?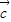 ).
).