题目内容
直线L1：ax+3y+1=0，L2：2x+（a+1）y+1=0，若L1∥L2，则a的值为（ ）A．-3
B．2
C．-3或2
D．3或-2
【答案】分析：由题意可知直线L1：ax+3y+1=0，斜率存在，直线L2：2x+（a+1）y+1=0，斜率相等求出a的值．
解答：解：直线L1：ax+3y+1=0的斜率为：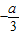
，直线L1∥L2，所以L2：2x+（a+1）y+1=0的斜率为：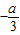
所以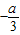
=
；
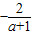解得a=-3，a=2（舍去）
故选A．
点评：本题考查两条直线平行的判定，两条直线平行与倾斜角、斜率的关系，考查计算能力，推理能力，是基础题．
解答：解：直线L1：ax+3y+1=0的斜率为：
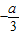，直线L1∥L2，所以L2：2x+（a+1）y+1=0的斜率为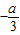：所以
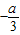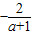=；解得a=-3，a=2（舍去）
故选A．
点评：本题考查两条直线平行的判定，两条直线平行与倾斜角、斜率的关系，考查计算能力，推理能力，是基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目