题目内容
函数f（x）=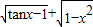
的定义域为 ．
【答案】分析：由题意可得 tanx≥1，且 x2≤1，即 kπ+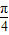
≤x＜kπ+
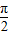，k∈z，且-1≤x≤1．由此求得函数f（x）=
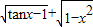的定义域．
解答：解：∵函数f（x）=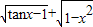
，
∴tanx≥1，且 x2≤1，即 kπ+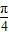
≤x＜kπ+
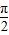，k∈z，且-1≤x≤1．
解得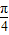
≤x≤1，
故答案为[
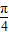，1]．
点评：本题主要考查求正切函数的定义域，函数的定义域以及求法，属于基础题．
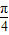≤x＜kπ+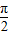，k∈z，且-1≤x≤1．由此求得函数f（x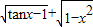）=的定义域．解答：解：∵函数f（x）=
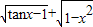，∴tanx≥1，且 x2≤1，即 kπ+
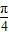≤x＜kπ+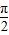，k∈z，且-1≤x≤1．解得
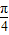≤x≤1，故答案为[
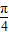，1]．点评：本题主要考查求正切函数的定义域，函数的定义域以及求法，属于基础题．
练习册系列答案
怎样学好牛津英语系列答案
相关题目