题目内容
已知定点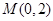 ,
,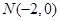 ,直线
,直线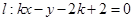 (
(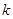 为常数).
为常数).
(1)若点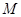 、
、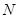 到直线
到直线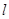 的距离相等,求实数
的距离相等,求实数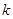 的值;
的值;
(2)对于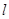 上任意一点
上任意一点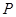 ,
,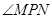 恒为锐角,求实数
恒为锐角,求实数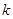 的取值范围.
的取值范围.
【答案】
(1) 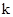 的值为1或
的值为1或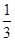 .(2)
.(2) 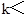
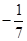 或k>1.
或k>1.
【解析】
试题分析:(1)根据点M,N到直线l的距离相等,可得l∥MN或l过MN的中点.
按l∥MN、l过MN的中点讨论得到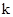 的值为1或
的值为1或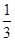 .
.
本题难度不大,但易于出现漏解现象.
(2)根据∠MPN恒为锐角,得知l与以MN为直径的圆相离,即圆心到直线l的距离大于半径,从而建立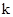 的不等式而得解.
的不等式而得解.
试题解析:(1)∵点M,N到直线l的距离相等,
∴l∥MN或l过MN的中点.
∵M(0,2),N(-2,0),
∴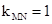 ,MN的中点坐标为C(-1,1).
,MN的中点坐标为C(-1,1).
又∵直线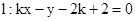 过点D(2,2),
过点D(2,2),
当l∥MN时,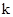 =kMN=1,
=kMN=1,
当l过MN的中点时,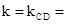
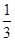 ,
,
综上可知: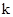 的值为1或
的值为1或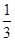 .
.
(2)∵对于l上任意一点P,∠MPN恒为锐角,
∴l与以MN为直径的圆相离,即圆心到直线l的距离大于半径, 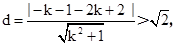
解得: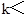
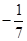 或k>1.
或k>1.
考点:距离,直线与圆的位置关系.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
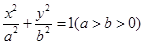 的离心率为
的离心率为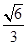 ,过
,过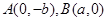 的直线与原点的距离为
的直线与原点的距离为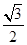
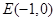 ,直线
,直线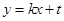 与椭圆交于不同两点C,D,试问:对任意的
与椭圆交于不同两点C,D,试问:对任意的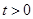 ,是否都存在实数
,是否都存在实数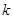 ,使得以线段CD为直径的圆过点E?证明你的结论
,使得以线段CD为直径的圆过点E?证明你的结论