题目内容
设函数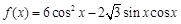 .
.
(1)求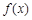 的最小正周期和值域;
的最小正周期和值域;
(2)在锐角△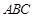 中,角
中,角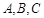 的对边分别为
的对边分别为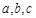 ,若
,若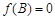 且
且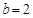 ,
,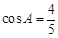 ,求
,求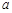 和
和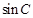 .
.
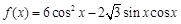 .
.(1)求
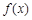 的最小正周期和值域;
的最小正周期和值域;(2)在锐角△
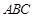 中,角
中,角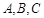 的对边分别为
的对边分别为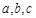 ,若
,若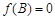 且
且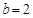 ,
,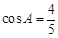 ,求
,求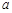 和
和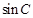 .
.(1) ,
, ,(2)
,(2) ,
, .
.
 ,
, ,(2)
,(2) ,
, .
.试题分析:(1)要研究三角函数的性质,首先先将三角函数化为
 型.利用降幂公式
型.利用降幂公式 及倍角公式
及倍角公式 可将函数次数化为一次,再利用配角公式
可将函数次数化为一次,再利用配角公式 化为
化为 ,然后利用基本三角函数图像求其最小正周期和值域,(2)解三角形问题,一般利用正余弦定理解决.本题为已知两角及一对边,选用正弦定理.由于是锐角△
,然后利用基本三角函数图像求其最小正周期和值域,(2)解三角形问题,一般利用正余弦定理解决.本题为已知两角及一对边,选用正弦定理.由于是锐角△ ,开方时取正.
,开方时取正.试题解析:(1)
 =
=
=
 . 3分
. 3分所以
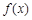 的最小正周期为
的最小正周期为 , 4分
, 4分值域为
 . 6分
. 6分(2)由
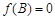 ,得
,得 .
. 为锐角,∴
为锐角,∴ ,
, ,∴
,∴ . 9分
. 9分∵
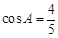 ,
, ,∴
,∴ . 10分
. 10分在△ABC中,由正弦定理得
 . 12分
. 12分∴
 . 14分
. 14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 所对的边分别为
所对的边分别为 ,且
,且 .
. 的大小;
的大小; ,求边
,求边 的值.
的值. 中,
中, 分别是角
分别是角 的对边,且
的对边,且 .
. 的大小;
的大小; ,求
,求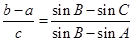 ,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.
,关于x的不等式x2cosC+4xsinC+6≥0对任意的x∈R恒成立.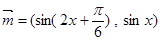 ,
, ,
,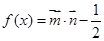 .
.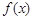 的单调递减区间;
的单调递减区间; 中,
中,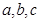 分别是角
分别是角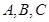 的对边,
的对边, ,
,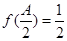 ,
, ,求
,求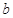 的大小.
的大小. 中,
中, ,则角
,则角 的取值范围是( )
的取值范围是( )



 .
.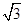 ,求a、b;
,求a、b;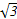 bc,sinC=2
bc,sinC=2 ,C=300,BC=3,则AB等于 .
,C=300,BC=3,则AB等于 .