Question

等轴双曲线的两个顶点分别为A₁、A₂,垂直于双曲线实轴的直线与双曲线交于M、N两点,求证：

(1)∠MA₁N+∠MA₂N=180°;

(2)MA₁⊥A₂N,MA₂⊥A₁N.

Answer 1

证明:(1)不妨设等轴双曲线的方程为,设直线MN的方程为x=b(b＞a).

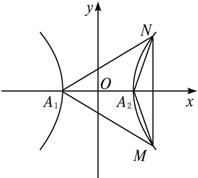
如图,易求得

∴,

.

∴

.

又∠NA₁x,∠NA₂x均为锐角,

∴∠NA₁x=90°-∠NA₂x,

即∠NA₁x+∠NA₂x=90°.

根据对称性,∴∠NA₁M+∠NA₂M=180°.

(2)仿(1)可求得.

∴.

∴MA₁⊥A₂N.

同理可证MA₂⊥A₁N.