题目内容
(本题满分12分)
已知数列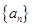 的前
的前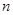 和为
和为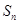 ,其中
,其中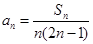 且
且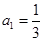
(1)求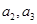
(2)猜想数列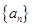 的通项公式,并用数学归纳法加以证明.
的通项公式,并用数学归纳法加以证明.
【答案】
解:(1)
又 ,则
,则 ,类似地求得
,类似地求得
(2)由 ,
, ,
, …
…
猜得: ;证明见解析.
;证明见解析.
【解析】本试题主要是考查了数列的归纳猜想的思想的运用,以及运用数学归纳法证明猜想的结论的综合运用。
(1)利用通项公式和前n项和的关系式,对n令值,分别得到前几项。
(2)根据前几项,归纳猜想其通项公式,并运用数学归纳法,分为两步来证明。
解:(1)
又 ,则
,则 ,类似地求得
,类似地求得
(2)由 ,
, ,
, …
…
猜得:
以数学归纳法证明如下:
① 当 时,由(1)可知等式成立;
时,由(1)可知等式成立;
②假设当 时猜想成立,即
时猜想成立,即
那么,当 时,由题设
时,由题设 得
得
 ,
,
所以
 =
=
 =
=


 -
-
因此,
所以

这就证明了当 时命题成立.
时命题成立.
由①、②可知命题对任何 都成立.
都成立.

练习册系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面