题目内容
(本小题满分10分)已知二次函数 满足条件
满足条件 ,及
,及 .
.
(1)求 的解析式;
的解析式;
(2)求 在
在 上的最值.
上的最值.
(1) ;(2)f(x)min=f(
;(2)f(x)min=f( )=
)= ,f(x)max=f(-1)=3.
,f(x)max=f(-1)=3.
【解析】
试题分析:(1)用待定系数法设出二次函数的解析式,根据条件列出三个系数的关系式并求解;
(2)先判断二次函数的对称轴为x= ,从而判断函数在区间
,从而判断函数在区间 上的单调情况,再求出何时取到最大值和最小值.
上的单调情况,再求出何时取到最大值和最小值.
试题解析:(1)设 ,
, 则
则


∴由题 c=1 ,2ax+a+b=2x 恒成立
∴ 2a=2 ,a+b=0, c=1 得 a=1 b=-1 c=1 ∴
(2) 在
在 单调递减,在
单调递减,在 单调递增
单调递增
∴f(x)min=f( )=
)= ,f(x)max=f(-1)=3.
,f(x)max=f(-1)=3.
考点:待定系数法求二次函数解析式,根据函数的单调性求函数最值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 则实数
则实数 的值是( )
的值是( ) B.2 C.
B.2 C. D.4
D.4  ,
, ,则
,则 的最小值是( )
的最小值是( ) B.
B. C.
C. D.
D.
 ,则
,则 的最小值是 .
的最小值是 . 中,
中, +
+ +
+ =12,那么
=12,那么 +
+ +
+ + +
+ + =
= ,函数
,函数 ,若实数m,n满足f(m)>f(n),则m,n的大小关系为________.
,若实数m,n满足f(m)>f(n),则m,n的大小关系为________.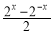 是( )
是( ) 满足线性约束条件
满足线性约束条件

 的取值范围是 .
的取值范围是 .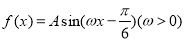 相邻两个对称轴之间的距离是
相邻两个对称轴之间的距离是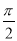 ,且满足,
,且满足, .
. 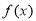 的单调递减区间;
的单调递减区间;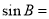
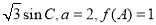 ,求△ABC的面积。
,求△ABC的面积。