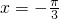题目内容
已知函数y=4cos2x+4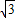 sinxcosx-2,(x∈R).
sinxcosx-2,(x∈R).(1)求函数的最小正周期;
(2)求函数的最大值及其相对应的x值;
(3)写出函数的单调增区间.
【答案】分析:(1)利用二倍角的余弦与正弦可将函数y=4cos2x+4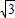 sinxcosx-2转化为y=4sin(2x+
sinxcosx-2转化为y=4sin(2x+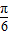 ),利用三角函数的周期公式即可求得函数的最小正周期;
),利用三角函数的周期公式即可求得函数的最小正周期;
(2)利用正弦函数的性质可求ymax,由2x+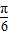 =2kπ+
=2kπ+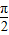 (k∈Z)可求其取最大值时相对应的x值;
(k∈Z)可求其取最大值时相对应的x值;
(3)利用正弦函数的单调性即可求得函数y=4cos2x+4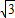 sinxcosx-2的单调增区间.
sinxcosx-2的单调增区间.
解答:解:(1)∵y=4cos2x+4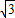 sinxcosx-2
sinxcosx-2
=2(1+cos2x)+2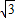 sn2x-2
sn2x-2
=2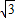 sin2x+2cos2x
sin2x+2cos2x
=4(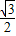 sin2x+
sin2x+ cos2x)
cos2x)
=4sin(2x+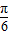 ),
),
∴其最小正周期T=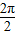 =π;
=π;
(2)当2x+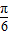 =2kπ+
=2kπ+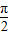 (k∈Z),即x=kπ+
(k∈Z),即x=kπ+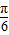 (k∈Z)时,ymax=4;
(k∈Z)时,ymax=4;
(3)由2kπ-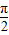 ≤2x+
≤2x+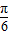 ≤2kπ+
≤2kπ+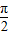 (k∈Z),
(k∈Z),
得-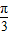 +kπ≤x≤
+kπ≤x≤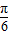 +kπ(k∈Z),
+kπ(k∈Z),
∴函数y=4cos2x+4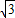 sinxcosx-2的单调增区间为[-
sinxcosx-2的单调增区间为[-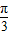 +kπ,
+kπ,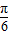 +kπ](k∈Z).
+kπ](k∈Z).
点评:本题考查二倍角的余弦与正弦,考查正弦函数的单调性与最值,考查三角函数的周期及其求法,属于中档题.
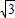 sinxcosx-2转化为y=4sin(2x+
sinxcosx-2转化为y=4sin(2x+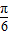 ),利用三角函数的周期公式即可求得函数的最小正周期;
),利用三角函数的周期公式即可求得函数的最小正周期;(2)利用正弦函数的性质可求ymax,由2x+
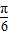 =2kπ+
=2kπ+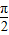 (k∈Z)可求其取最大值时相对应的x值;
(k∈Z)可求其取最大值时相对应的x值;(3)利用正弦函数的单调性即可求得函数y=4cos2x+4
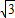 sinxcosx-2的单调增区间.
sinxcosx-2的单调增区间.解答:解:(1)∵y=4cos2x+4
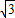 sinxcosx-2
sinxcosx-2=2(1+cos2x)+2
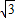 sn2x-2
sn2x-2=2
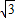 sin2x+2cos2x
sin2x+2cos2x=4(
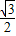 sin2x+
sin2x+ cos2x)
cos2x)=4sin(2x+
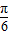 ),
),∴其最小正周期T=
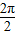 =π;
=π;(2)当2x+
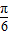 =2kπ+
=2kπ+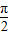 (k∈Z),即x=kπ+
(k∈Z),即x=kπ+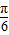 (k∈Z)时,ymax=4;
(k∈Z)时,ymax=4;(3)由2kπ-
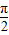 ≤2x+
≤2x+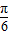 ≤2kπ+
≤2kπ+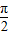 (k∈Z),
(k∈Z),得-
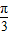 +kπ≤x≤
+kπ≤x≤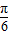 +kπ(k∈Z),
+kπ(k∈Z),∴函数y=4cos2x+4
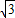 sinxcosx-2的单调增区间为[-
sinxcosx-2的单调增区间为[-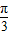 +kπ,
+kπ,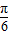 +kπ](k∈Z).
+kπ](k∈Z).点评:本题考查二倍角的余弦与正弦,考查正弦函数的单调性与最值,考查三角函数的周期及其求法,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
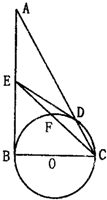 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. 
 )的图象经过点(0,2),则不是该函数的一条对称轴方程为
)的图象经过点(0,2),则不是该函数的一条对称轴方程为