题目内容
已知a、b∈(0,+∞),且a+b=1,求证:(a+
思路解析:由条件可以考虑三角换元,也可以考虑求出 证法一:∵a+b=1∴ (a+ = 证法二:∵a+b=1,a>0,b>0, ∴a+b≥2 由此可得 证法三:欲证原不等式成立, 需证4(ab)2+4(a2+b2)-25ab+4≥0,即4(ab)2+4(1-2ab)-25ab+4≥0,亦即4(ab)2-33ab+8≥0.∴ab≤ ∵a+b=1,a>0,b>0,∴ab≥8,不可能.∵1=a+b≥2 证法四:∵a>0,b>0,a+b=1,令a=sin2α,b=cos2α,α∈(0, (a+ = 证法五:∵a+b=1,a>0,b>0,∴a+b≥2 ∴(a+
![]() 的范围,或者考虑用判别式法,等等.
的范围,或者考虑用判别式法,等等.![]() ≤
≤![]() =
=![]() ,
,![]() )(a+
)(a+![]() )=
)=![]() +
+![]() +ab+
+ab+![]()
![]() +
+![]() +(
+(![]() -
-![]() )2+2≥2+(2-
)2+2≥2+(2-![]() )2+2=
)2+2=![]() .
.![]() .∴ab≤
.∴ab≤![]() .∴(1-ab)2≥(1-
.∴(1-ab)2≥(1-![]() )2=
)2=![]() .
.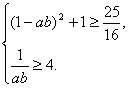 ∴
∴![]() ≥
≥![]() ,即(a+
,即(a+![]() )(a+
)(a+![]() )≥
)≥![]() .
.![]() 或ab≥8.
或ab≥8.![]() ,∴ab≤
,∴ab≤![]() 成立,故得证.
成立,故得证.![]() ),则
),则![]() )(a+
)(a+![]() )=(sin2α+
)=(sin2α+![]() )(cos2α+
)(cos2α+![]() )=
)=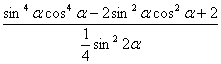
![]() ≥
≥![]() =
=![]() .
.![]() .∴ab≤
.∴ab≤![]() .
.![]() )(a+
)(a+![]() )-
)-![]() =
=![]() ·
·![]() -
-![]() =
=![]() =
=![]() ≥0,故(a+
≥0,故(a+![]() )(a+
)(a+![]() )≥
)≥![]() .
. 练习册系列答案
练习册系列答案
导学与评估测评卷系列答案
初中总复习同步指导训练与检测系列答案
快乐口算系列答案
决胜百分百系列答案
小升初真题精选系列答案
基础天天练系列答案
夺冠训练归类模拟总复习系列答案
天府优学系列答案
小升初模拟冲刺卷系列答案
新考题大集结系列答案
相关题目
已知|
|=2|
|≠0,且关于x的函数f(x)=
x3+
|
|x2+
•
x在R上有极值,则
与
的夹角范围为( )
| a |
| b |
| 1 |
| 3 |
| 1 |
| 2 |
| a |
| a |
| b |
| a |
| b |
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|