题目内容
某厂家为调查一种新推出的产品的颜色接受程度是否与性别有关,数据如下表:
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
根据表中的数据,得到k=![]() ≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
考点:
独立性检验.
专题:
计算题;概率与统计.
分析:
由题意k≈10.653,根据临界值表中所给的概率,得到与本题所得的数据对应的概率P(K2≥7.879)=0.005,由此得到本题答案.
解答:
解:提出假设H0:产品的颜色接受程度与性别没有关系
根据表中的数据,得到 k=![]() ≈10.653
≈10.653
对照临界值表可以得到P(K2≥7.879)=0.005
∵题中K2≈10.653≥7.879,
∴当H0成立时,K2≥7.879的概率约为0.005,
因此我们有99.5%的把握认为产品的颜色接受程度与性别有关系
这种判断出错的可能性是0.005
故答案为:0.005
点评:
独立性检验是考查两个分类变量是否有关系,并且能较精确的给出这种判断的可靠程度的一种重要的统计方法,主要是通过k2的观测值与临界值的比较加以解决的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某厂家为调查一种新推出的产品的颜色接受程度是否与性别有关,数据如下表:
根据表中的数据,得到k=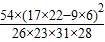 ≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
| 黑 | 红 | |
| 男 | 17 | 9 |
| 女 | 6 | 22 |
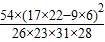 ≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .
≈10.653,因为K2≥7.879,所以产品的颜色接受程度与性别有关系,那么这种判断出错的可能性为 .