题目内容
已知F1、F2是双曲线
的两焦点，以线段F1F2为边作正三角形，若双曲线恰好平分正三角形的另两边，则双曲线的离心率是________．
分析：根据双曲线的对称性可推断出三角形的顶点在y轴，根据正三角形的性质求得顶点的坐标，进而求得正三角形的边与双曲线的交点，代入双曲线方程与b2=c2-a2联立整理求得e．
解答：双曲线恰好平分正三角形的另两边，
顶点就在Y轴上坐标是（0，
c）或（0，-c）那么正三角形的边与双曲线的交点就是边的中点（
，
c）在双曲线上代入方程
-
=1联立 b2=c2-a2求得e4-8e2+4=0
求得e=
+1 故答案为：
+1点评：本题主要考查了双曲线的简单性质．考查了学生对双曲线基础知识的综合把握．
练习册系列答案
相关题目
已知F1，F2分别为双曲
-
=1(a＞0，b＞0)的左、右焦点，P为双曲线左支上任一点，若
的最小值为8a，则双曲线的离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| |PF2|2 |
| |PF1| |
| A、（1，+∞） |
| B、（0，3] |
| C、（1，3] |
| D、（0，2] |
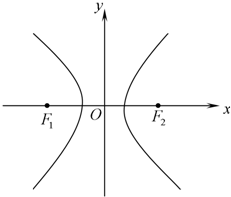
的左、右两个焦点，点P是双曲线上一点，且|PF1|．|PF2|=32，求∠F1PF2的大小．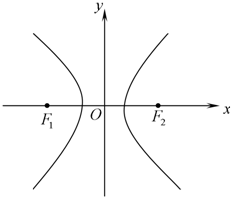
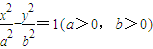的左、右焦点，P为双曲线左支上任一点，若
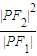的最小值为8a，则双曲线的离心率e的取值范围是（ ）
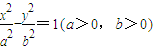的左、右焦点，P为双曲线左支上任一点，若
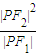的最小值为8a，则双曲线的离心率e的取值范围是（ ）