题目内容
以抛物线的焦点弦AB为直径的圆与准线的位置关系( )A.相交
B.相切
C.相离
D.不能确定
【答案】分析:设抛物线为标准抛物线:y2=2px(p>0 ),过焦点的弦为PQ,PQ的中点是M且到准线的距离是d.设P到准线的距离d1=|PF|,Q到准线的距离d2=|AB|.结合中位线的定义与抛物线的定义可得: =
=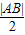 ,等于半径,进而得到答案.
,等于半径,进而得到答案.
解答:解:不妨设抛物线为标准抛物线:y2=2px (p>0 ),即抛物线位于y轴的右侧,以x轴为对称轴.
由于过焦点的弦为AB,AB的中点是M,M到准线的距离是d.
而A到准线的距离d1=|AF|,Q到准线的距离d2=|BF|.
又M到准线的距离d是梯形的中位线,故有d=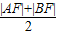 ,
,
由抛物线的定义可得: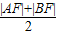 =
=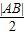 ,等于半径.
,等于半径.
所以圆心M到准线的距离等于半径,所以圆与准线是相切.
故选B.
点评:本题主要考查抛物线的性质应用,解决此类问题的关键是熟练掌握抛物线的定义,以及直线与圆的位置关系的判定,属于中档题.
 =
=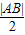 ,等于半径,进而得到答案.
,等于半径,进而得到答案.解答:解:不妨设抛物线为标准抛物线:y2=2px (p>0 ),即抛物线位于y轴的右侧,以x轴为对称轴.
由于过焦点的弦为AB,AB的中点是M,M到准线的距离是d.
而A到准线的距离d1=|AF|,Q到准线的距离d2=|BF|.
又M到准线的距离d是梯形的中位线,故有d=
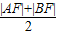 ,
,由抛物线的定义可得:
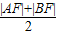 =
=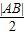 ,等于半径.
,等于半径.所以圆心M到准线的距离等于半径,所以圆与准线是相切.
故选B.
点评:本题主要考查抛物线的性质应用,解决此类问题的关键是熟练掌握抛物线的定义,以及直线与圆的位置关系的判定,属于中档题.

练习册系列答案
相关题目