Question

【题目】如图，在郊野公园的景观河的两岸，、是夹角为120°的两条岸边步道（长度均超过千米），为方便市民观光游览，现准备在河道拐角处的另一侧建造一个观景台，在两条步道、上分别设立游客上下点、，从、到观景台建造两条游船观光线路、，测得千米.

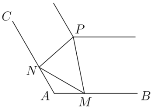
（1）求游客上下点、间的距离；

（2）若，设，求两条观光线路与之和关于的表达式，并求其最大值.

Answer 1

【答案】（1）3千米；（2），最大值是6.

【解析】

（1）在三角形AMN中，利用余弦定理即可得解；

（2）利用正弦定理，表示出，进行三角恒等变换即可得解.

（1）在三角形AMN中，由余弦定理可得：

，

所以游客上下点、间的距离为3千米；

（2）若，设，

三角形中，由正弦定理可得：，

所以

即，

当时，取得最大值6.