题目内容
3.已知点F1(-2,0),F2(2,0),动点P满足|PF2|-|PF1|=2,当点P的纵坐标为3时,P到两定点F1,F2的距离之和|PF1|+|PF2|等于8.分析 运用双曲线的定义,可得动点P的轨迹为焦点在x轴上的双曲线的左支,求得a,b,c.得到双曲线的方程,再令y=3,解方程求得P的横坐标,再由两点的距离公式,计算即可得到答案.
解答 解:点F1(-2,0),F2(2,0),
则|F1F2|=4,
由动点P满足|PF2|-|PF1|=2<4,
由双曲线的定义可得,动点P的轨迹为焦点在x轴上的双曲线的左支,
且a=1,c=2,则b=$\sqrt{{c}^{2}-{a}^{2}}=\sqrt{4-1}=\sqrt{3}$,即有x2-$\frac{{y}^{2}}{3}$=1(x<0).
令y=3,则x2=1+3=4,解得,x=-2,∴P(-2,3).
则|PF1|+|PF2|=$\sqrt{(-2+2)^{2}+(3-0)^{2}}+\sqrt{(-2-2)^{2}+(3-0)^{2}}$=8.
故答案为:8.
点评 本题考查双曲线的定义和方程,考查运算能力,属于基础题.

练习册系列答案
相关题目
14.已知正项等比数列{an},且a2a10=2a52,a3=1,则a4=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
11.已知a>0,不等式组$\left\{\begin{array}{l}{x≥0}\\{y≤0}\\{y≥a(x-2)}\end{array}\right.$,表示的平面区域的面积为1,则a的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
18.不等式($\frac{1}{3}$)x-1≤0的解集是( )
| A. | (-∞,1] | B. | (-∞,0] | C. | [1,+∞) | D. | [0,+∞) |
8.已知α是第二象限角,则2α的终边在( )
| A. | 第一、二象限 | B. | 第二象限 | C. | 第三、四象限 | D. | 以上都不对 |
10.已知数列{an}满足a1=b(b>0),an+1(an+1)=-1(n∈N*),则使得an=b的n的值可以为( )
| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
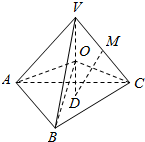 如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M.
如图所示,正四面体V-ABC的高VD的中点为O,VC的中点为M. ,则
,则 等于
等于 B.
B. C.
C. D.
D.