题目内容
数列{an}中,如果存在ak,使得“ak>ak-1且ak>ak+1”成立(其中k≥2,k∈N*),则称ak为{an}的一个峰值.(Ⅰ)若
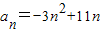 ,则{an}的峰值为 ;
,则{an}的峰值为 ;(Ⅱ)若an=tlnn-n,且an不存在峰值,则实数 t的取值范围是 .
【答案】分析:(Ⅰ)可以令f(n)=an=-3n2+11n,利用数列的函数特性,可以判定函数的单调性及其最值问题;
(Ⅱ)若an=tlnn-n,且an不存在峰值,即不存在最值,从而求出实数t的取值范围;
解答:解:(Ⅰ)若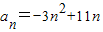 ,可以令f(n)=-3n2+11n,图象开口向下,
,可以令f(n)=-3n2+11n,图象开口向下,
可得f(n)=-3n2+11n=-3(n-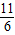 )2+
)2+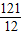
可以存在n=2,使得a2=-3×4+11×2=10,对于任意的n∈N都有,an≤2,
可得{an}的峰值为10;
(Ⅱ)若an=tlnn-n,a1=-1,a2=tln2-2,a3=tln3-3,ak=tlnk-k
可以令g(x)=tlnx-x,g′(x)=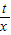 -1=
-1=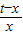 ,(x>t)
,(x>t)
∵若an=tlnn-n,且an不存在峰值,即不存在先增后减的情况,
即a1≥a2,-1≥tln2-2,解得t≤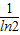 ,
,
还有另外一种情况,后面每一项在t的调节下都相等,an不存在峰值,
即an=an+1,∴tlnn-n=tln(n+1)-(n+1),
解得t=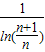 ,n≥2,n∈N*,
,n≥2,n∈N*,
综上可得:{t|t≤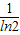 或t=
或t=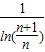 ,n≥2,n∈N*},
,n≥2,n∈N*},
故答案为:10,{t|t≤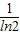 或t=
或t=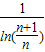 ,n≥2,n∈N*};
,n≥2,n∈N*};
点评:此题主要考查数列函数的特性,是一道中档题,考查的知识点比较全面,考查了利用导数研究函数的单调性;
(Ⅱ)若an=tlnn-n,且an不存在峰值,即不存在最值,从而求出实数t的取值范围;
解答:解:(Ⅰ)若
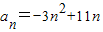 ,可以令f(n)=-3n2+11n,图象开口向下,
,可以令f(n)=-3n2+11n,图象开口向下,可得f(n)=-3n2+11n=-3(n-
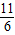 )2+
)2+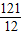
可以存在n=2,使得a2=-3×4+11×2=10,对于任意的n∈N都有,an≤2,
可得{an}的峰值为10;
(Ⅱ)若an=tlnn-n,a1=-1,a2=tln2-2,a3=tln3-3,ak=tlnk-k
可以令g(x)=tlnx-x,g′(x)=
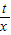 -1=
-1=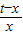 ,(x>t)
,(x>t)∵若an=tlnn-n,且an不存在峰值,即不存在先增后减的情况,
即a1≥a2,-1≥tln2-2,解得t≤
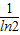 ,
,还有另外一种情况,后面每一项在t的调节下都相等,an不存在峰值,
即an=an+1,∴tlnn-n=tln(n+1)-(n+1),
解得t=
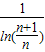 ,n≥2,n∈N*,
,n≥2,n∈N*,综上可得:{t|t≤
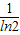 或t=
或t=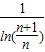 ,n≥2,n∈N*},
,n≥2,n∈N*},故答案为:10,{t|t≤
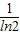 或t=
或t=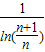 ,n≥2,n∈N*};
,n≥2,n∈N*};点评:此题主要考查数列函数的特性,是一道中档题,考查的知识点比较全面,考查了利用导数研究函数的单调性;

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
在数列{an}中,如果an+1=
an+1,(n∈N*),且a1=1,则a4等于( )
| 1 |
| 2 |
| A、4 | ||
B、
| ||
C、
| ||
D、
|