题目内容
如图,在正方体中,O是下底面的中心,B′H⊥D′O,H为垂足,求证:
(1)A′C′∥平面ABCD;
(2)AC⊥平面BB′D′D
(3)B′H⊥平面AD′C.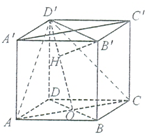
(1)A′C′∥平面ABCD;
(2)AC⊥平面BB′D′D
(3)B′H⊥平面AD′C.

证明:(1)由正方体可得AA′
CC′,∴四边形ACC′A′是平行四边形,∴A′C′∥AC.
∵AC?ABCD,A′C′?平面ABCD.
∴A′C′∥平面ABCD;
(2)由正方体的性质可得BB′⊥平面ABCD,
∴BB′⊥AC.
由正方形ABCD可得AC⊥BD,
∵BD∩BB′=B.
∴AC⊥平面BB′D′D.
(3)由(2)可得:AC⊥平面BB′D′D,
∴AC⊥B′H.
又B′H⊥D′O.AC∩OD′=O,
∴B′H⊥平面AD′C.
| ∥ |
| . |
∵AC?ABCD,A′C′?平面ABCD.
∴A′C′∥平面ABCD;
(2)由正方体的性质可得BB′⊥平面ABCD,
∴BB′⊥AC.
由正方形ABCD可得AC⊥BD,
∵BD∩BB′=B.
∴AC⊥平面BB′D′D.
(3)由(2)可得:AC⊥平面BB′D′D,
∴AC⊥B′H.
又B′H⊥D′O.AC∩OD′=O,
∴B′H⊥平面AD′C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在正方体中,O是下底面的中心,B′H⊥D′O,H为垂足,求证:
如图,在正方体中,O是下底面的中心,B′H⊥D′O,H为垂足,求证: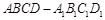 中,E、F、G分别为
中,E、F、G分别为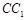 、
、 、
、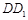 的中点,O为
的中点,O为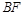 与
与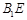 的交点,
的交点,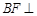 面
面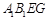
 与平面
与平面
