ЬтФПФкШн
ЁОЬтФПЁПДгФГбЇаЃИпШ§ФъМЖЙВ![]() УћФаЩњжаЫцЛњГщШЁ
УћФаЩњжаЫцЛњГщШЁ![]() УћВтСПЩэИпЃЌВтСПЗЂЯжБЛВтбЇЩњЩэИпШЋВПНщгк
УћВтСПЩэИпЃЌВтСПЗЂЯжБЛВтбЇЩњЩэИпШЋВПНщгк![]() КЭ
КЭ![]() жЎМфЃЌНЋВтСПНсЙћАДШчЯТЗНЪНЗжГЩАЫзщЃЌЕквЛзщ
жЎМфЃЌНЋВтСПНсЙћАДШчЯТЗНЪНЗжГЩАЫзщЃЌЕквЛзщ![]() ЃЛЕкЖўзщ
ЃЛЕкЖўзщ![]() ЃЌ
ЃЌ![]() ЃЌЕкАЫзщ
ЃЌЕкАЫзщ![]() ЃЌШчЭМЪЧАДЩЯЪіЗжзщЗНЗЈЕУЕНЕФЦЕТЪЗжВМжБЗНЭМЕФвЛВПЗжЃЌШєЕквЛзщгыЕкАЫзщШЫЪ§ЯрЭЌЃЌЕкСљзщЁЂЕкЦпзщЁЂЕкАЫзщШЫЪ§вРДЮЙЙГЩЕШВюЪ§СаЃЎ
ЃЌШчЭМЪЧАДЩЯЪіЗжзщЗНЗЈЕУЕНЕФЦЕТЪЗжВМжБЗНЭМЕФвЛВПЗжЃЌШєЕквЛзщгыЕкАЫзщШЫЪ§ЯрЭЌЃЌЕкСљзщЁЂЕкЦпзщЁЂЕкАЫзщШЫЪ§вРДЮЙЙГЩЕШВюЪ§СаЃЎ

ЃЈ![]() ЃЉЙРМЦетЫљбЇаЃИпШ§ФъМЖШЋЬхФаЩњЩэИп
ЃЉЙРМЦетЫљбЇаЃИпШ§ФъМЖШЋЬхФаЩњЩэИп![]() вдЩЯЃЈКЌ
вдЩЯЃЈКЌ![]() ЃЉЕФШЫЪ§ЃЎ
ЃЉЕФШЫЪ§ЃЎ
ЃЈ![]() ЃЉЧѓЕкСљзщЁЂЕкЦпзщЕФЦЕТЪВЂВЙГфЭъећЦЕТЪЗжВМжБЗНЭМЃЎЃЈЧІБЪзїЭМВЂгУжаадБЪУшКкЃЉЃЎ
ЃЉЧѓЕкСљзщЁЂЕкЦпзщЕФЦЕТЪВЂВЙГфЭъећЦЕТЪЗжВМжБЗНЭМЃЎЃЈЧІБЪзїЭМВЂгУжаадБЪУшКкЃЉЃЎ
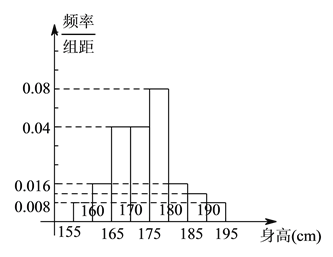
ЃЈ![]() ЃЉШєДгЩэИпЪєгкЕкСљзщКЭЕкАЫзщЕФЫљгаФаЩњжаЫцЛњГщШЁСНУћФаЩњЃЌМЧЫћУЧЕФЩэИпЗжБ№ЮЊ
ЃЉШєДгЩэИпЪєгкЕкСљзщКЭЕкАЫзщЕФЫљгаФаЩњжаЫцЛњГщШЁСНУћФаЩњЃЌМЧЫћУЧЕФЩэИпЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЃЌЧѓТњзу
ЃЌЧѓТњзу![]() ЕФЪТМўИХТЪЃЎ
ЕФЪТМўИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ9ШЫЃЛЃЈ2ЃЉМћНтЮіЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгЩЦЕТЪЗжВМжБЗНЭМПЩЕУЧАЮхзщЦЕТЪЃЌНјЖјПЩЕУКѓШ§зщЦЕТЪКЭШЫЪ§ЃЌгжПЩЕУКѓШ§зщЕФШЫЪ§ЃЌПЩЕУЦНОљЩэИпЃЛ
ЃЈ2ЃЉвзЕУКѓШ§зщЕФ![]() ЃЌПЩЕУЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЌПЩЕУЦЕТЪЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉгЩЃЈ![]() ЃЉжЊЩэИпдк
ЃЉжЊЩэИпдк![]() ФкЕФШЫЪ§ЮЊ
ФкЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЃЩэИпЮЊ
ЁЃЩэИпЮЊ![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ЩшЮЊ![]() ЃЌ
ЃЌ![]() ЃЎЃЌСаОйПЩЕУзмЕФЛљБОЪТМўЙВ15жжЧщПіЃЌЪТМўЁА
ЃЎЃЌСаОйПЩЕУзмЕФЛљБОЪТМўЙВ15жжЧщПіЃЌЪТМўЁА![]() ЁБЫљАќКЌЕФЛљБОЪТМўИіЪ§га6+1=7ЃЌгЩИХТЪЙЋЪНПЩЕУЃЎ
ЁБЫљАќКЌЕФЛљБОЪТМўИіЪ§га6+1=7ЃЌгЩИХТЪЙЋЪНПЩЕУЃЎ
ЪдЬтНтЮіЃКЃЈ![]() ЃЉгЩЦЕТЪЗжВМжБЗНЭМжЊЃЌ
ЃЉгЩЦЕТЪЗжВМжБЗНЭМжЊЃЌ
ЧАЮхзщЦЕТЪЮЊ![]() ЃЌ
ЃЌ
КѓШ§зщЦЕТЪЮЊ![]() ЃЌШЫЪ§ЮЊ
ЃЌШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
етЫљбЇаЃИпШ§ФаЩњЩэИпдк![]() вдЩЯЃЈКЌ
вдЩЯЃЈКЌ![]() ЃЉЕФШЫЪ§ЮЊ
ЃЉЕФШЫЪ§ЮЊ![]() ШЫЃЎ
ШЫЃЎ
ЃЈ![]() ЃЉгЩЦЕТЪЗжВМжБЗНЭМЕУЕкАЫзщЦЕТЪЮЊ
ЃЉгЩЦЕТЪЗжВМжБЗНЭМЕУЕкАЫзщЦЕТЪЮЊ![]() ЃЌШЫЪ§ЮЊ
ЃЌШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ЩшЕкСљзщШЫЪ§ЮЊ![]() ЃЌдђЕкЦпзщШЫЪ§ЮЊ
ЃЌдђЕкЦпзщШЫЪ§ЮЊ![]() ЃЌгж
ЃЌгж![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
МДЕкСљзщШЫЪ§ЮЊ![]() ШЫЃЌЕкЦпзщШЫЪ§ЮЊ
ШЫЃЌЕкЦпзщШЫЪ§ЮЊ![]() ШЫЃЌЦЕТЪЗжБ№ЮЊ
ШЫЃЌЦЕТЪЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЦЕТЪГ§вдзщОрЗжБ№ЕШгк![]() ЃЌ
ЃЌ![]() ЃЌМћЭМЃЎ
ЃЌМћЭМЃЎ
ЃЈ![]() ЃЉгЩЃЈ
ЃЉгЩЃЈ![]() ЃЉжЊЩэИпдк
ЃЉжЊЩэИпдк![]() ФкЕФШЫЪ§ЮЊ
ФкЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
Щш![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЃЩэИпЮЊ
ЁЃЩэИпЮЊ![]() ЕФШЫЪ§ЮЊ
ЕФШЫЪ§ЮЊ![]() ШЫЃЌ
ШЫЃЌ
ЩшЮЊ![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
Шє![]() ЃЌ
ЃЌ![]() ЪБЃЌга
ЪБЃЌга![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВСљжжЧщПіЃЎ
ЙВСљжжЧщПіЃЎ
Шє![]() ЃЌ
ЃЌ![]() ЪБЃЌга
ЪБЃЌга![]() ЙВвЛжжЧщПіЃЎ
ЙВвЛжжЧщПіЃЎ
Шє![]() ЃЌ
ЃЌ![]() ЗжБ№дк
ЗжБ№дк![]() ЃЌ
ЃЌ![]() ФкЪБЃЌ
ФкЪБЃЌ
га![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЙВ
ЙВ![]() жжЧщПіЃЎ
жжЧщПіЃЎ
ЫљвдЛљБОЪТМўЕФзмЪ§ЮЊ![]() жжЃЎ
жжЃЎ
ЪТМў![]() ЫљАќКЌЕФЛљБОЪТМўИіЪ§га
ЫљАќКЌЕФЛљБОЪТМўИіЪ§га![]() жжЃЌЙЪ
жжЃЌЙЪ![]() ЃЎ
ЃЎ

ЁОЬтФПЁПФГаЃЮЊСЫНтИпвЛЪЕбщАрЕФЪ§бЇГЩМЈ,ВЩгУГщбљЕїВщЕФЗНЪН,ЛёШЁСЫ![]() ЮЛбЇЩњдкЕквЛбЇЦкФЉЕФЪ§бЇГЩМЈЪ§Он,бљБОЭГМЦНсЙћШчЯТБэЃК
ЮЛбЇЩњдкЕквЛбЇЦкФЉЕФЪ§бЇГЩМЈЪ§Он,бљБОЭГМЦНсЙћШчЯТБэЃК
Зжзщ | ЦЕЪ§ | ЦЕТЪ |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
КЯМЦ |
|
|
(1)Чѓ![]() ЕФжЕКЭЪЕбщАрЪ§бЇЦНОљЗжЕФЙРМЦжЕЃЛ
ЕФжЕКЭЪЕбщАрЪ§бЇЦНОљЗжЕФЙРМЦжЕЃЛ
(2)ШчЙћгУЗжВуГщбљЕФЗНЗЈДгЪ§бЇГЩМЈаЁгк![]() ЗжЕФбЇЩњжаГщШЁ
ЗжЕФбЇЩњжаГщШЁ![]() УћбЇЩњ,дйДгет
УћбЇЩњ,дйДгет![]() УћбЇЩњжабЁ
УћбЇЩњжабЁ![]() ШЫ,ЧѓжСЩйгавЛИібЇЩњЕФЪ§бЇГЩМЈЪЧдк
ШЫ,ЧѓжСЩйгавЛИібЇЩњЕФЪ§бЇГЩМЈЪЧдк![]() ЕФИХТЪ.
ЕФИХТЪ.

