题目内容
(本小题满分10分)
如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器 已知喷水器的喷水区域是半径为5 m的圆 问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
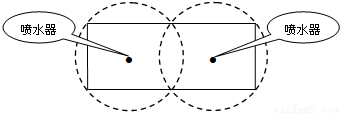
花坛长为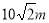 ,宽为
,宽为 ,两喷水器位于矩形分成的两个正方形的中心,则符合要求;
,两喷水器位于矩形分成的两个正方形的中心,则符合要求;
【解析】
试题分析:由题可知,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界,则有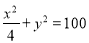
使花坛的面积最大且能全部喷到水,则问题转化为在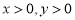 ,
,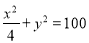 的条件下,求
的条件下,求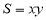 的最大值。此时有两种方法求最值,法一采用的是基本不等式法,法二采用的是二次函数求最值的方法,两种方法求最值,同学们都应该掌握。
的最大值。此时有两种方法求最值,法一采用的是基本不等式法,法二采用的是二次函数求最值的方法,两种方法求最值,同学们都应该掌握。
试题解析:设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界 依题意得: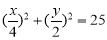 ,(
,(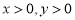 )
)
问题转化为在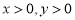 ,
,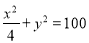 的条件下,求
的条件下,求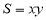 的最大值 4分
的最大值 4分
法一: ,
,
由 和
和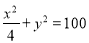 及
及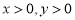 得:
得: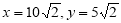
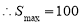
法二:∵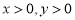 ,
,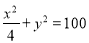 ,
,
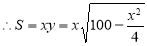 =
=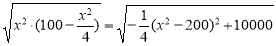
∴当 ,即
,即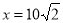 ,
,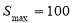
由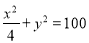 可解得:
可解得: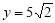 8分
8分
答:花坛的长为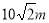 ,宽为
,宽为 ,两喷水器位于矩形分成的两个正方形的中心,则符合要求 10分
,两喷水器位于矩形分成的两个正方形的中心,则符合要求 10分
考点:①利用基本不等式求最值②利用配方法求最值

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 ,
, , 若
, 若 方向相反, 则实数
方向相反, 则实数 的值是( )
的值是( ) B.
B. C.
C. D.
D.
 ,
, ,
, ,则
,则 B.
B. C.
C. D.
D.
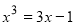 的三根
的三根 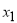 ,
,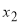 ,
,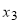 ,其中
,其中 B.(0 , 1 ) C.(1,
B.(0 , 1 ) C.(1, 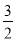 ) D.(
) D.( ,则
,则 的大小关系是
的大小关系是 B.
B. C.
C. D.
D.
 的解集为____________
的解集为____________  中,对任意
中,对任意 ,
, ,则
,则 等于
等于 B.
B. C.
C. D.
D.
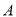 ,
,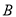 都在平面
都在平面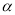 内,定点
内,定点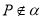 ,
,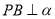 ,
,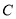 是
是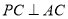 .那么,动点C在平面
.那么,动点C在平面