题目内容
设向量a=(m,2-m2),b=(cosθ,γ+sinθ),其中m、γ、θ∈R,已知a=2b,求λ的取值范围.
解法1:∵a=2b,∴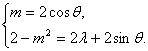
于是λ=1-2cos2θ-sinθ=2sin2θ-sinθ-1=2(sinθ-![]() )2-
)2-![]() .
.
当sinθ=![]() 时,λ取最小值-
时,λ取最小值-![]() ,当sinθ=-1时,λ取最大值2.所以λ的取值范围是[-
,当sinθ=-1时,λ取最大值2.所以λ的取值范围是[-![]() ,2].
,2].
解法2:∵a=2b,∴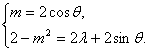 ∴
∴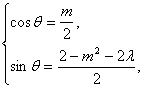
∴![]() +
+![]() =1,
=1,
∴m4-(3-4λ)m2+4λ2-8λ=0.
设t=m2,则0≤t≤4,令f(t)=t2-(3-4λ)t+4λ2-8λ,
则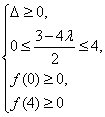 或f(0)·f(4)≤0,
或f(0)·f(4)≤0,
∴ 或0≤λ≤2.
或0≤λ≤2.
∴-![]() ≤λ≤0或0≤λ≤2.故λ的取值范围是[-
≤λ≤0或0≤λ≤2.故λ的取值范围是[-![]() ,2].
,2].

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设向量
=(m,3),
=(-1,2),
∥
,则实数m的值为( )
| a |
| b |
| a |
| b |
| A、2 | ||
| B、6 | ||
C、
| ||
D、-
|