题目内容
证明函数f(x)=x6-x3+x2-x+1的值恒为正数.
证明：当x＜0时，f(x)各项都为正数，因此，x＜0,x=1时，f(x)＞0,
当0≤x≤1时,f(x)=x6+x2(1-x)+(1-x)＞0，
当x＞1时，f(x)=x3(x3-1)+x(x-1)+1＞0，
综上所述，函数f(x)的值恒为正数.
练习册系列答案
相关题目
探究函数f(x)=x+
，x∈(0，+∞)的最小值，并确定取得最小值时x的值．列表如下：
请观察表中y值随x值变化的特点，完成以下的问题．
（1）函数f(x)=x+
(x＞0)在区间（0，2）上递减，函数f(x)=x+
(x＞0)在区间 上递增；
（2）函数f(x)=x+
(x＞0)，当x= 时，y最小= ；
（3）函数f(x)=x+
(x＜0)时，有最值吗？是最大值还是最小值？此时x为何值？（直接回答结果，不需证明）
| 4 |
| x |
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.002 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
（1）函数f(x)=x+
| 4 |
| x |
| 4 |
| x |
（2）函数f(x)=x+
| 4 |
| x |
（3）函数f(x)=x+
| 4 |
| x |
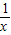是奇函数”的证明不是综合法的是（ ）
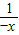=-（x+
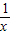）=-f（x），∴f（x）是奇函数
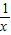+（-x）+（-
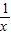）=0，∴f（x）=-f（-x），∴f（x）是奇函数
=
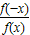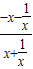=-1，∴f（-x）=-f（x），∴f（x）是奇函数
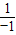=-2，又f（1）=1+
=2