题目内容
观察1=1,3+5=8,7+9+11=27,13+15+17+19=64,…,猜想一般规律是________________.
[n(n-1)+1]+[n(n-1)+3]+[n(n-1)+5]+…+[n(n-1)+(2n-1)]=n3
分析:1
3+5
7+9+11
13+15+17+19
……
每个和式的第一个数是1,3,7,13,…,
构成数列{an},则有
an+1-an=2n.
∴
∴an-a1=2+4+…+2(n-1)=2(1+2+…+n-1)=n(n-1).
∴an=n2-n+1.
又每个和式中的项构成公差为2的等差数列.
∴一般规律是[n(n-1)+1]+[n(n-1)+3]+[n(n-1)+5]+…+[n(n-1)+(2n-1)]=n·[n(n-1)+1]+2×![]() =n3.
=n3.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
(本题满分12分)探究函数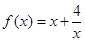 ,
,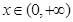 的最小值,并确定取得最小值时
的最小值,并确定取得最小值时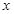 的值,列表如下:
的值,列表如下:
|
|
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
|
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中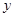 值随
值随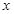 值变化的特点,完成下列问题:
值变化的特点,完成下列问题:
(1) 当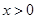 时,
时,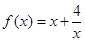 在区间
在区间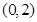 上递减,在区间 上递增;
上递减,在区间 上递增;
所以,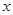 =
时,
=
时, 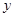 取到最小值为
;
取到最小值为
;
(2) 由此可推断,当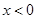 时,
时,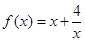 有最
值为 ,此时
有最
值为 ,此时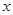 =
;
=
;
(3) 证明: 函数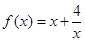 在区间
在区间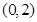 上递减;
上递减;
(4) 若方程 在
在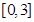 内有两个不相等的实数根,求实数
内有两个不相等的实数根,求实数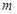 的取值范围。
的取值范围。