题目内容
在△ABC中,∠A=60°,b=1,s△ABC=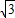 ,则△ABC外接圆的半径R= .
,则△ABC外接圆的半径R= .
【答案】分析:利用三角形面积公式,求出c,再利用余弦定理可得a的值,利用2R=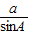 ,即可求得结论.
,即可求得结论.
解答:解:由题意,∵S△ABC=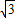 =
= ×1×c×sin60°,∴c=4,
×1×c×sin60°,∴c=4,
由余弦定理可得a2=b2+c2-2bc•cos60°=13,
∴a=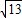 ,∴2R=
,∴2R=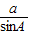 =
=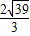
∴R=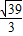
故答案为: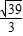
点评:本题考查正弦定理、余弦定理的应用,考查学生的计算能力,属于基础题.
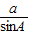 ,即可求得结论.
,即可求得结论.解答:解:由题意,∵S△ABC=
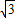 =
= ×1×c×sin60°,∴c=4,
×1×c×sin60°,∴c=4,由余弦定理可得a2=b2+c2-2bc•cos60°=13,
∴a=
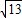 ,∴2R=
,∴2R=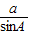 =
=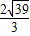
∴R=
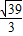
故答案为:
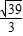
点评:本题考查正弦定理、余弦定理的应用,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目