Question

求下列函数的反函数:

(1)y=+2；

(2)y=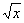

(3)f(x)=－x²+2x－5(x≤1).

Answer 1

解:(1)函数y=+2的值域为{y|y≥2}.

由y=+2得x=(y－2)².

∴函数y=+2的反函数为y=(x－2)²(x≥2).

(2)当0≤x<1时，由y=x²－1得－1≤y<0，且x=.

当－1≤x<0时，由y=x²得0<y≤1，且x=－.

∴函数y=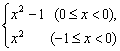的反函数为

y=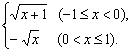

(3)∵y=－(x－1)²－4(x≤1),

∴此函数图象是顶点为(1，－4)、开口向下的抛物线.

由x≤1知，函数的值域为{y|y≤－4}.

由解析式y=－(x－1)²－4,得

x－1=－.

对换x、y得f^－1(x)=1－.

∴所求反函数为f^－1(x)=1－  (x≤－4).

点评:确定函数就是确定函数的对应关系和定义域，求函数的反函数也是求反函数的解析式和反函数的定义域，特别要注意反函数的定义域就是原来函数的值域.求出反函数后必须注明其定义域，分段函数求反函数，就是对各段分别求反函数.求反函数的方法是依据反函数定义，步骤是:(1)由原函数解析式及定义域求出其值域.(2)由y=f(x)解出x=f^－1(y).(3)对换x、y改写成反函数表达式y=f^－1(x),并注明其定义域.