题目内容
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°.(1)求四棱锥P-ABCD的体积;
(2)若E是PB的中点,求异面直线DE与PA所成角的大小(结果用反三角函数值表示).
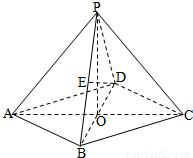
【答案】分析:(1)由PO⊥平面ABCD,得∠PBO是PB与平面ABCD所成的角,∠PBO=60°.由此我们可以计算出PO即棱锥的高,及底面菱形的面积,代入即可得到棱锥的体积.
(2)求异面直线DE与PA所成角的大小有两种不同的思路:法一是以O为坐标原点,射线OB、OC、OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.表示出空间中各个点的坐标,进而给出相关向量的坐标,然后利用异面直线的夹角的余弦等于其方向向量夹角余弦值的绝对值,求出夹角.
法二是取AB的中点F,连接EF、DF.由E是PB的中点,得EF∥PA,则∠FED是异面直线DE与PA所成角(或它的补角),然后解三角形FED求出夹角.
解答:解:(1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得
∠PBO是PB与平面ABCD所成的角,∠PBO=60°.
在Rt△AOB中BO=ABsin30°=1,由PO⊥BO,
于是,PO=BOtan60°=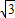 ,而底面菱形的面积为2
,而底面菱形的面积为2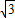 .
.
∴四棱锥P-ABCD的体积V= ×2
×2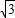 ×
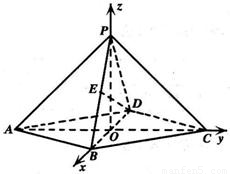
×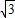 =2.
=2.
(2)解法一:以O为坐标原点,射线OB、OC、
OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.
在Rt△AOB中OA=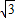 ,于是,点A、B、
,于是,点A、B、
D、P的坐标分别是A(0,-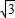 ,0),
,0),
B(1,0,0),D(-1,0,0),P(0,0,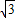 ).
).
E是PB的中点,则E( ,0,
,0,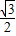 )于是
)于是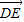 =(
=( ,0,
,0,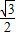 ),
),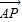 =(0,
=(0,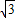 ,
,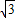 ).
).
设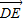 与
与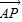 的夹角为θ,有cosθ=
的夹角为θ,有cosθ=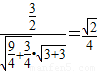 ,θ=arccos
,θ=arccos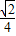 ,
,
∴异面直线DE与PA所成角的大小是arccos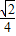 ;
;
解法二:取AB的中点F,连接EF、DF.
由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成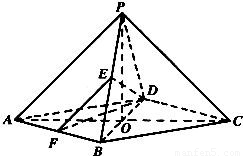
角(或它的补角),
在Rt△AOB中AO=ABcos30°=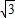 =OP,
=OP,
于是,在等腰Rt△POA中,
PA=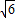 ,则EF=
,则EF=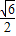 .
.
在正△ABD和正△PBD中,DE=DF=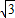 ,
,
cos∠FED=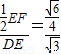 =
=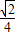
∴异面直线DE与PA所成角的大小是arccos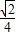 .
.
点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值.
(2)求异面直线DE与PA所成角的大小有两种不同的思路:法一是以O为坐标原点,射线OB、OC、OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.表示出空间中各个点的坐标,进而给出相关向量的坐标,然后利用异面直线的夹角的余弦等于其方向向量夹角余弦值的绝对值,求出夹角.
法二是取AB的中点F,连接EF、DF.由E是PB的中点,得EF∥PA,则∠FED是异面直线DE与PA所成角(或它的补角),然后解三角形FED求出夹角.
解答:解:(1)在四棱锥P-ABCD中,由PO⊥平面ABCD,得
∠PBO是PB与平面ABCD所成的角,∠PBO=60°.
在Rt△AOB中BO=ABsin30°=1,由PO⊥BO,
于是,PO=BOtan60°=
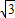 ,而底面菱形的面积为2
,而底面菱形的面积为2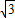 .
.∴四棱锥P-ABCD的体积V=
 ×2
×2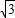 ×
×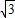 =2.
=2.(2)解法一:以O为坐标原点,射线OB、OC、
OP分别为x轴、y轴、z轴的正半轴建立空间直角坐标系.

在Rt△AOB中OA=
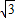 ,于是,点A、B、
,于是,点A、B、D、P的坐标分别是A(0,-
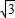 ,0),
,0),B(1,0,0),D(-1,0,0),P(0,0,
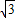 ).
).E是PB的中点,则E(
 ,0,
,0,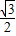 )于是
)于是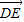 =(
=( ,0,
,0,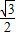 ),
),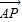 =(0,
=(0,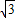 ,
,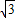 ).
).设
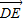 与
与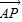 的夹角为θ,有cosθ=
的夹角为θ,有cosθ=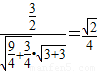 ,θ=arccos
,θ=arccos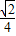 ,
,∴异面直线DE与PA所成角的大小是arccos
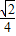 ;
;解法二:取AB的中点F,连接EF、DF.
由E是PB的中点,得EF∥PA,
∴∠FED是异面直线DE与PA所成

角(或它的补角),
在Rt△AOB中AO=ABcos30°=
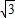 =OP,
=OP,于是,在等腰Rt△POA中,
PA=
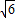 ,则EF=
,则EF=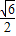 .
.在正△ABD和正△PBD中,DE=DF=
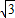 ,
,cos∠FED=
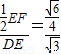 =
=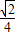
∴异面直线DE与PA所成角的大小是arccos
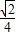 .
.点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,