ĢāÄæÄŚČŻ
”¾ĢāÄæ”æŌŚµ³ÖŠŃėµÄÕżČ·Įģµ¼ĻĀ£¬ĶعżČ«¹śČĖĆńµÄĘėŠÄŠĮ¦£¬ĢŲ±šŹĒČ«ĢåŅ»ĻßŅ½»¤ČĖŌ±µÄ·ÜĮ¦¾ČÖĪ£¬¶žŌĀ·Ż”°ŠĀ¹Ś·ĪŃ×”±ŅßĒéµĆµ½ĮĖæŲÖĘ£®¼×”¢ŅŅĮ½øöµŲĒų²ÉČ”·Ą»¤“ėŹ©ŗó£¬Ķ³¼ĘĮĖ“Ó2ŌĀ7ČÕµ½2ŌĀ13ČÕŅ»ÖܵĊĀŌö”°ŠĀ¹Ś·ĪŃ×”±Č·ÕļČĖŹż£¬»ęÖĘ³ÉČēĻĀÕŪĻßĶ¼£ŗ
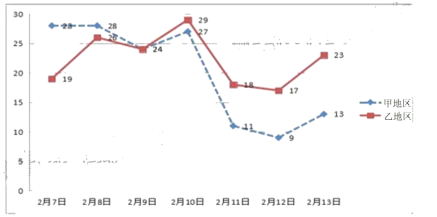
£Ø1£©øł¾ŻĶ¼ÖŠ¼×”¢ŅŅĮ½øöµŲĒųÕŪĻßĶ¼µÄŠÅĻ¢£¬Š“³öÄćČĻĪŖ×īÖŲŅŖµÄĮ½øöĶ³¼Ę½įĀŪ£»
£Ø2£©ÖĪĮĘ”°ŠĀ¹Ś·ĪŃ×”±Ņ©Ę·µÄŃŠ·¢³ÉĮĖµ±ĪńÖ®¼±£¬Ä³Ņ©Ęó¼Ę»®¶Ō¼×µŲĒųµÄ![]() ĻīÄæ»ņŅŅµŲĒųµÄ
ĻīÄæ»ņŅŅµŲĒųµÄ![]() ĻīÄæĶ¶ČėŃŠ·¢×Ź½š£¬¾¹żĘĄ¹Ą£¬¶ŌÓŚ
ĻīÄæĶ¶ČėŃŠ·¢×Ź½š£¬¾¹żĘĄ¹Ą£¬¶ŌÓŚ![]() ĻīÄ棬ĆæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóŹĒl.38ĶņŌŖ”¢1.18ĶņŌŖ”¢l.14ĶņŌŖµÄøÅĀŹ·Ö±šĪŖ
ĻīÄ棬ĆæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóŹĒl.38ĶņŌŖ”¢1.18ĶņŌŖ”¢l.14ĶņŌŖµÄøÅĀŹ·Ö±šĪŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() £»¶ŌÓŚ
£»¶ŌÓŚ![]() ĻīÄ棬ĄūČóÓė²śĘ·¼ŪøńµÄµ÷ÕūÓŠ¹Ų£¬ŅŃÖŖ
ĻīÄ棬ĄūČóÓė²śĘ·¼ŪøńµÄµ÷ÕūÓŠ¹Ų£¬ŅŃÖŖ![]() ĻīÄæ²śĘ·¼ŪøńŌŚŅ»ÄźÄŚ½ųŠŠ2“Ī¶ĄĮ¢µÄµ÷Õū£¬Ćæ“Ī¼Ūøńµ÷ÕūÖŠ£¬²śĘ·¼ŪøńĻĀµ÷µÄøÅĀŹ¶¼ŹĒ
ĻīÄæ²śĘ·¼ŪøńŌŚŅ»ÄźÄŚ½ųŠŠ2“Ī¶ĄĮ¢µÄµ÷Õū£¬Ćæ“Ī¼Ūøńµ÷ÕūÖŠ£¬²śĘ·¼ŪøńĻĀµ÷µÄøÅĀŹ¶¼ŹĒ![]() £¬¼Ē
£¬¼Ē![]() ĻīÄæŅ»ÄźÄŚ²śĘ·¼ŪøńµÄĻĀµ÷“ĪŹżĪŖ
ĻīÄæŅ»ÄźÄŚ²śĘ·¼ŪøńµÄĻĀµ÷“ĪŹżĪŖ![]() £¬ĆæĶ¶×ŹŹ®ĶņŌŖ£¬
£¬ĆæĶ¶×ŹŹ®ĶņŌŖ£¬![]() Č”0”¢1”¢2Ź±£¬Ņ»ÄźŗóĻąÓ¦ĄūČóŹĒ1.4ĶņŌŖ”¢1.25ĶņŌŖ”¢0.6ĶņŌŖ£®¼Ē¶Ō
Č”0”¢1”¢2Ź±£¬Ņ»ÄźŗóĻąÓ¦ĄūČóŹĒ1.4ĶņŌŖ”¢1.25ĶņŌŖ”¢0.6ĶņŌŖ£®¼Ē¶Ō![]() ĻīÄæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóµÄĖ껜±äĮæĪŖ
ĻīÄæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóµÄĖ껜±äĮæĪŖ![]() £¬¼Ē¶Ō
£¬¼Ē¶Ō![]() ĻīÄæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóµÄĖ껜±äĮæĪŖ
ĻīÄæĶ¶×ŹŹ®ĶņŌŖ£¬Ņ»ÄźŗóĄūČóµÄĖ껜±äĮæĪŖ![]() £®
£®
(i)Ēó![]() £¬
£¬![]() µÄøÅĀŹ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū
µÄøÅĀŹ·Ö²¼ĮŠŗĶŹżŃ§ĘŚĶū![]() £¬
£¬![]() £»
£»
(ii)Čē¹ūÄćŹĒĶ¶×Ź¾ö²ßÕߣ¬½«×ö³öŌõŃłµÄ¾ö²ß?ĒėŠ“³ö¾ö²ßĄķÓÉ£®
”¾“š°ø”æ£Ø1£©¢Ł¼×µŲĒų±ČŅŅµŲĒųµÄŠĀŌöČĖŹżµÄĘ½¾łŹżµĶ£» ¢Ś¼×µŲĒų±ČŅŅµŲĒųµÄ·½²ī“ó£»
£Ø2£©(i)·Ö²¼ĮŠ¼ū½āĪö£¬![]() =1.2£¬
=1.2£¬![]()
![]() £» (ii) µ±
£» (ii) µ±![]() Ź±£¬Ķ¶×Ź
Ź±£¬Ķ¶×Ź![]() ĻīÄ棻µ±
ĻīÄ棻µ±![]() Ź±£¬Į½øöĻīÄ涼æÉŅŌ£»µ±
Ź±£¬Į½øöĻīÄ涼æÉŅŌ£»µ±![]() Ź±£¬Ķ¶×Ź
Ź±£¬Ķ¶×Ź![]() ĻīÄ森ĄķÓɼū½āĪö
ĻīÄ森ĄķÓɼū½āĪö
”¾½āĪö”æ
£Ø1£©ÓÉĶ¼±ķæÉÖŖ¼×µŲĒųµÄŹż¾Ż±Č½Ļ·ÖÉ¢£¬ĖłŅŌ¼×µŲĒų±ČŅŅµŲĒųµÄ·½²ī“ó£»Ņ²æÉĒó³öĮ½µŲĒųµÄĘ½¾łŹż£¬±Č½ĻĘ½Ōö¶ąŹż£»
£Ø2£©£Øi£©ÓÉĢāæÉÖŖ![]() ·Ö±šČ”l.38”¢1.18”¢l.14Ź±£¬Ęä¶ŌÓ¦µÄøÅĀŹ·Ö±šĪŖ
·Ö±šČ”l.38”¢1.18”¢l.14Ź±£¬Ęä¶ŌÓ¦µÄøÅĀŹ·Ö±šĪŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬“Ó¶ųæÉĮŠ³ö
£¬“Ó¶ųæÉĮŠ³ö![]() µÄ·Ö²¼ĮŠ£¬ÓÉĢāŅāµĆ
µÄ·Ö²¼ĮŠ£¬ÓÉĢāŅāµĆ![]() £¬“Ó¶ųæÉĮŠ³ö
£¬“Ó¶ųæÉĮŠ³ö![]() µÄ·Ö²¼ĮŠ£¬¶ų
µÄ·Ö²¼ĮŠ£¬¶ų![]() Č”0”¢1”¢2Ź±£¬Ņ»ÄźŗóĻąÓ¦ĄūČóŹĒ1.4ĶņŌŖ”¢1.25ĶņŌŖ”¢0.6ĶņŌŖ£¬ÓÉ“ĖæÉĮŠ³ö
Č”0”¢1”¢2Ź±£¬Ņ»ÄźŗóĻąÓ¦ĄūČóŹĒ1.4ĶņŌŖ”¢1.25ĶņŌŖ”¢0.6ĶņŌŖ£¬ÓÉ“ĖæÉĮŠ³ö![]() µÄ·Ö²¼ĮŠ£¬²¢æÉĒó³öĘŚĶū£»
µÄ·Ö²¼ĮŠ£¬²¢æÉĒó³öĘŚĶū£»
£Øii£©¶Ō£Øi£©µĆµ½µÄŹżŃ§ĘŚĶū![]() £¬
£¬![]() ±Č½Ļ“󊔣¬½ųŠŠ¾ö²ß.
±Č½Ļ“󊔣¬½ųŠŠ¾ö²ß.
£Ø1£©¢Ł¼×µŲĒų±ČŅŅµŲĒųµÄŠĀŌöČĖŹżµÄĘ½¾łŹżµĶ£»
¢Ś¼×µŲĒų±ČŅŅµŲĒųµÄ·½²ī“ó£»
£Ø2£©£Øi£©ÓÉĢāŅāµĆ![]() µÄøÅĀŹ·Ö²¼ĮŠĪŖ
µÄøÅĀŹ·Ö²¼ĮŠĪŖ
| 1.38 | 1.18 | 1.14 |
|
|
|
|
ĖłŅŌ![]() £®
£®
ÓÉĢāŅāµĆ![]() £¬¼“
£¬¼“![]() µÄøÅĀŹ·Ö²¼ĮŠĪŖ
µÄøÅĀŹ·Ö²¼ĮŠĪŖ
| 0 | 1 | 2 |
|
|
|
|
ÓÉĢāŅāµĆĻĀµ÷“ĪŹż![]() ŗĶĄūČó
ŗĶĄūČó![]() µÄ¹ŲĻµĪŖ
µÄ¹ŲĻµĪŖ
| 0 | 1 | 2 |
| 1.4 | 1.25 | 0.6 |
ĖłŅŌ![]() µÄøÅĀŹ·Ö²¼ĮŠĪŖ
µÄøÅĀŹ·Ö²¼ĮŠĪŖ
| 1.4 | 1.25 | 0.6 |
|
|
|
|
ĖłŅŌ![]()
![]()
![]()
£Øii£©µ±![]() £¬µĆ
£¬µĆ![]() £¬¼“
£¬¼“![]() £¬
£¬
ÕūĄķµĆ![]() £¬½āµĆ
£¬½āµĆ![]() £»
£»
µ±![]() Ź±£¬
Ź±£¬![]() £»
£»
µ±![]() Ź±£¬
Ź±£¬![]() £»
£»
ĖłŅŌ£¬µ±![]() Ź±£¬Ķ¶×Ź
Ź±£¬Ķ¶×Ź![]() ĻīÄ棻µ±
ĻīÄ棻µ±![]() Ź±£¬Į½øöĻīÄ涼æÉŅŌ£»µ±
Ź±£¬Į½øöĻīÄ涼æÉŅŌ£»µ±![]() Ź±£¬Ķ¶×Ź
Ź±£¬Ķ¶×Ź![]() ĻīÄ森
ĻīÄ森

 ĆūŠ£æĪĢĆĻµĮŠ“š°ø
ĆūŠ£æĪĢĆĻµĮŠ“š°ø”¾ĢāÄæ”æÄ³Ę¶Ą§µŲĒų¹²ÓŠ1500»§¾ÓĆń£¬ĘäÖŠĘ½ŌµŲĒų1050»§£¬É½Ēų450»§.ĪŖµ÷²éøƵŲĒų2017Äź¼ŅĶ„ŹÕČėĒéæö£¬“Ó¶ųøüŗƵŲŹµŹ©”°¾«×¼·öʶ”±£¬²ÉÓĆ·Ö²ć³éŃłµÄ·½·Ø£¬ŹÕ¼ÆĮĖ150»§¼ŅĶ„2017ğğŹÕČėµÄŃł±¾Źż¾Ż£Øµ„Ī»£ŗĶņŌŖ£©.

£Ø1£©Ó¦ŹÕ¼Æ¶ąÉŁ»§É½Ēų¼ŅĶ„µÄŃł±¾Źż¾Ż£æ
£Ø2£©øł¾ŻÕā150øöŃł±¾Źż¾Ż£¬µĆµ½2017Äź¼ŅĶ„ŹÕČėµÄʵĀŹ·Ö²¼Ö±·½Ķ¼£ØČēĶ¼ĖłŹ¾£©£¬ĘäÖŠŃł±¾Źż¾Ż·Ö×éĒų¼äĪŖ£Ø0£¬0.5]£¬£Ø0.5£¬1]£¬£Ø1£¬1.5]£¬£Ø1.5£¬2]£¬£Ø2£¬2.5]£¬£Ø2.5£¬3].Čē¹ū½«ĘµĀŹŹÓĪŖøÅĀŹ£¬¹Ą¼ĘøƵŲĒų2017Äź¼ŅĶ„ŹÕČė³¬¹ż1.5ĶņŌŖµÄøÅĀŹ£»
£Ø3£©Ńł±¾Źż¾ŻÖŠ£¬ÓŠ5»§É½Ēų¼ŅĶ„µÄÄźŹÕČė³¬¹ż2ĶņŌŖ£¬ĒėĶź³É2017Äź¼ŅĶ„ŹÕČėÓėµŲĒųµÄĮŠĮŖ±ķ£¬²¢ÅŠ¶ĻŹĒ·ńÓŠ90%µÄ°ŃĪÕČĻĪŖ”°øƵŲĒų2017Äź¼ŅĶ„ÄźŹÕČėÓėµŲĒųÓŠ¹Ų”±£æ
³¬¹ż2ĶņŌŖ | ²»³¬¹ż2ĶņŌŖ | ×Ü¼Ę | |
Ę½ŌµŲĒų | |||
ɽĒų | 5 | ||
×Ü¼Ę |
ø½£ŗ
P£ØK2”Żk0£© | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
”¾ĢāÄæ”æŅŃÖŖĮ½øö·ÖĄą±äĮæXŗĶY£¬ÓÉĖūĆĒµÄ¹Ū²āŹż¾Ż¼ĘĖćµĆµ½K2µÄ¹Ū²āÖµ·¶Ī§ŹĒ3.841<k<6.635£¬¾ŻK2µÄĮŁ½ēÖµ±ķ£¬ŌņŅŌĻĀÅŠ¶ĻÕżČ·µÄŹĒ£Ø £©
![]()
P(K2”Żk) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.ŌŚ·ø“ķĪóøÅĀŹ²»³¬¹ż0.05µÄĒ°ĢįĻĀ£¬ČĻĪŖ±äĮæXÓėYÓŠ¹ŲĻµ
B.ŌŚ·ø“ķĪóøÅĀŹ²»³¬¹ż0.05µÄĒ°ĢįĻĀ£¬ČĻĪŖ±äĮæXÓėYƻӊ¹ŲĻµ
C.ŌŚ·ø“ķĪóøÅĀŹ²»³¬¹ż0.01µÄĒ°ĢįĻĀ£¬ČĻĪŖ±äĮæXÓėYÓŠ¹ŲĻµ
D.ŌŚ·ø“ķĪóøÅĀŹ²»³¬¹ż0.01µÄĒ°ĢįĻĀ£¬ČĻĪŖ±äĮæXÓėYƻӊ¹ŲĻµ