题目内容
已知△ABC的角A、B、C所对的边分别是a、b、c,设向量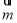 =(a,b),
=(a,b),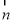 =(sin B,sin A),
=(sin B,sin A),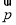 =(b-2,a-2).
=(b-2,a-2).
(Ⅰ)若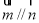 ,判断△ABC的形状;
,判断△ABC的形状;
(Ⅱ)若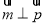 ,边长c=2,角C=
,边长c=2,角C=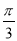 ,求△ABC的面积.
,求△ABC的面积.
练习册系列答案
相关题目
9.在极坐标系中,圆ρ=4cosθ(ρ∈R)的圆心到直线$θ=\frac{π}{3}$的距离是( )
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | 1 | D. | 2 |
商丘市某高中从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100),4.
(Ⅰ)请把给出的样本频率分布表中的空格都填上;
(Ⅱ)估计成绩在85分以上学生的比例;
(Ⅲ)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100)中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | 0.30 |
[80,90) | ||
[90,100) | 4 | 0.08 |
合计 |
20.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,A是双曲线C的左顶点,P(-$\frac{{a}^{2}}{c}$,yp)在双曲线的一条渐近线上,M为线段F1P的中点,且F1P⊥AM,则该双曲线C的渐近线为( )
| A. | y=±$\sqrt{3}$x | B. | y=±2x | C. | y=±$\sqrt{2}$x | D. | y=±$\sqrt{5}$x |


 满足
满足 则
则 的最大值等于( )
的最大值等于( ) B.
B. C.
C. D.
D.
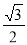 cos 2x的最小正周期和振幅分别是( )
cos 2x的最小正周期和振幅分别是( )