题目内容
条件甲:函数f(x)满足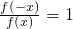 ;条件乙:函数f(x)是偶函数,则甲是乙的
;条件乙:函数f(x)是偶函数,则甲是乙的
- A.充分非必要条件
- B.必要非充分条件
- C.充要条件
- D.既非充分也非必要条件
A
分析:利用奇函数的定义“函数y=f(x)的定义域为D,如果对D内的任意一个x,都有x∈D,且f(-x)=f(x),则这个函数叫做偶函数”,针对于两个条件分析得到结论.
解答:条件甲:函数f(x)满足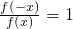 ,
,
即f(-x)=f(x)可以得到函数是一个偶函数
条件乙:函数f(x)是偶函数,一定要满足f(x)=f(-x),
但是不能保证两边同除以f(x)有意义,
∴条件甲是条件乙的充分非必要条件,
故选A
点评:本题主要考查了函数奇偶性的判断,以及必要条件、充分条件与充要条件的判断,本题解题的关键是对函数式要进行等价变形,本题属于基础题.
分析:利用奇函数的定义“函数y=f(x)的定义域为D,如果对D内的任意一个x,都有x∈D,且f(-x)=f(x),则这个函数叫做偶函数”,针对于两个条件分析得到结论.
解答:条件甲:函数f(x)满足
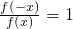 ,
,即f(-x)=f(x)可以得到函数是一个偶函数
条件乙:函数f(x)是偶函数,一定要满足f(x)=f(-x),
但是不能保证两边同除以f(x)有意义,
∴条件甲是条件乙的充分非必要条件,
故选A
点评:本题主要考查了函数奇偶性的判断,以及必要条件、充分条件与充要条件的判断,本题解题的关键是对函数式要进行等价变形,本题属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则条件甲是条件乙的( )
,则条件甲是条件乙的( )