题目内容
 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα=( )
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,若AD与平面AA1C1C所成的角为α,则sinα=( )分析:要求AD与平面AA1C1C所成的角,关键是找出AD在平面AA1C1C内的射影,利用正三棱柱的性质可得到线面角,解直角三角形求出此角的正弦值.
解答:解:如图,分别取C1A1、CA的中点E、F,连接B1E与BF,
∵三棱柱ABC-A1B1C1是正三棱柱
∴B1E⊥平面CAA1C1,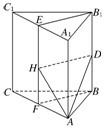
过D作DH∥B1E,则DH⊥平面CAA1C1,
连接AH,则∠DAH为所求的AD与平面AA1C1C所成的角
∵AB=1,D在棱BB1上,且BD=1
∴DH=B1E=
,DA=
,
所以sin∠DAH=
=
;
故选D.
∵三棱柱ABC-A1B1C1是正三棱柱
∴B1E⊥平面CAA1C1,

过D作DH∥B1E,则DH⊥平面CAA1C1,
连接AH,则∠DAH为所求的AD与平面AA1C1C所成的角
∵AB=1,D在棱BB1上,且BD=1
∴DH=B1E=
| ||
| 2 |
| 2 |
所以sin∠DAH=
| DH |
| DA |
| ||
| 4 |
故选D.
点评:本题以正三棱柱为载体,考查线面角,关键是找出AD在平面AA1C1C内的射影.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB,D是AC的中点.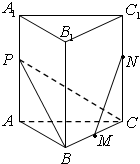 如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且
如图,在正三棱柱ABC-A1B1C1中,所有棱的长度都是1,M是BC边的中点,P是AA1边上的点,且 如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为
如图,在正三棱柱ABC-A'B'C'中,AB=2,若二面角C'-AB-C的大小为60°,则点C到平面ABC'的距离为