题目内容
对于函数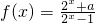 ,
,
(Ⅰ)求函数的定义域;
(Ⅱ)当a为何值时,f(x)为奇函数;
(Ⅲ)写出(Ⅱ)中函数的单调区间,并用定义给出证明.
(1)解:由题意可得,2x-1≠0 即x≠0
∴定义域为{x|x≠0}
(2)解:由f(x)是奇函数,则对任意x∈{x|x≠0}
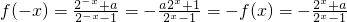
化简得(a-1)2x=a-1∴a=1
∴a=1时,f(x)是奇函数
(3)当a=1时,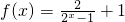 的单调递减区间为(-∞,0)和(0,+∞).
的单调递减区间为(-∞,0)和(0,+∞).
证明:任取x1,x2∈(0,+∞) 且x1<x2 则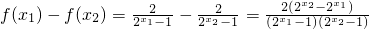
∵0<x1<x2 y=2x 在R上递增∴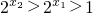
∴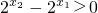 ,
,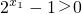 ,
,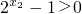
∴f(x1)-f(x2)>0∴f(x) 在(0,+∞) 上单调递减.同理:f(x) 在(-∞,0)上单调递减.
综上: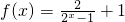 在(-∞,0)上单调递减,在(0,+∞) 上单调递减.
在(-∞,0)上单调递减,在(0,+∞) 上单调递减.
分析:(1)由题意可得,2x-1≠0 可求函数的定义域
(2)由题意可得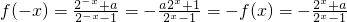 ,化简可求a
,化简可求a
(3)当a=1时,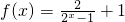 ,只要现证明,x∈(0,+∞)时的单调性,然后根据奇函数对称区间上的单调性相同可知,任取x1,x2∈(0,+∞) 且x1<x2 然后只要判断f(x1)与f(x2)的大小即可 证明
,只要现证明,x∈(0,+∞)时的单调性,然后根据奇函数对称区间上的单调性相同可知,任取x1,x2∈(0,+∞) 且x1<x2 然后只要判断f(x1)与f(x2)的大小即可 证明
点评:本题主要考查了奇函数的定义在参数求解中的应用,及函数的单调性的定义在函数证明中的应用,属于函数知识的综合应用.
∴定义域为{x|x≠0}
(2)解:由f(x)是奇函数,则对任意x∈{x|x≠0}
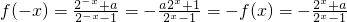
化简得(a-1)2x=a-1∴a=1
∴a=1时,f(x)是奇函数
(3)当a=1时,
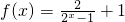 的单调递减区间为(-∞,0)和(0,+∞).
的单调递减区间为(-∞,0)和(0,+∞).证明:任取x1,x2∈(0,+∞) 且x1<x2 则
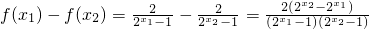
∵0<x1<x2 y=2x 在R上递增∴
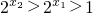
∴
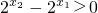 ,
,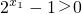 ,
,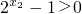
∴f(x1)-f(x2)>0∴f(x) 在(0,+∞) 上单调递减.同理:f(x) 在(-∞,0)上单调递减.
综上:
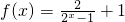 在(-∞,0)上单调递减,在(0,+∞) 上单调递减.
在(-∞,0)上单调递减,在(0,+∞) 上单调递减.分析:(1)由题意可得,2x-1≠0 可求函数的定义域
(2)由题意可得
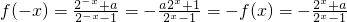 ,化简可求a
,化简可求a(3)当a=1时,
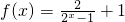 ,只要现证明,x∈(0,+∞)时的单调性,然后根据奇函数对称区间上的单调性相同可知,任取x1,x2∈(0,+∞) 且x1<x2 然后只要判断f(x1)与f(x2)的大小即可 证明
,只要现证明,x∈(0,+∞)时的单调性,然后根据奇函数对称区间上的单调性相同可知,任取x1,x2∈(0,+∞) 且x1<x2 然后只要判断f(x1)与f(x2)的大小即可 证明点评:本题主要考查了奇函数的定义在参数求解中的应用,及函数的单调性的定义在函数证明中的应用,属于函数知识的综合应用.

练习册系列答案
相关题目