题目内容
已知抛物线y2=-x与直线y=k(x+1)相交于A、B两点,O为坐标原点.(1)求证:OA⊥OB;
(2)当△OAB的面积为![]() 时,求k的值.
时,求k的值.
解:由直线的方程与抛物线的方程联立,可得 ∴xA·xB=( (1)由于yOA·yOB= (2)由弦长公式得 |AB|= 由点到直线的距离公式,得原点到AB的距离为d= 则S△AOB= ∴k=±
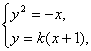 消去x,得ky2+y-k=0,由韦达定理,得yA·yB=-1,yA+yB=-
消去x,得ky2+y-k=0,由韦达定理,得yA·yB=-1,yA+yB=-![]() ,
,![]() -1)(
-1)(![]() -1)=
-1)=![]() -
-![]() +1=-
+1=-![]() +
+![]() +1=1.
+1=1.![]() ·
·![]() =-1,∴OA⊥OB.
=-1,∴OA⊥OB.![]() |yA-yB|=
|yA-yB|=![]() ·
·![]() =
=![]() ·
·![]() .
.![]() .
.![]() |AB|·d=
|AB|·d=![]() ·
·![]() ·
·![]() ·
·![]() =
=![]()
![]() =
=![]() .
.![]() .
. 练习册系列答案
练习册系列答案
寒假学习园地河南人民出版社系列答案

德华书业寒假训练营学年总复习安徽文艺出版社系列答案
阳光假日寒假系列答案
蓝天教育寒假优化学习系列答案
寒假专题集训系列答案
步步高寒假专题突破练黑龙江出版社系列答案
寒假自主学习手册系列答案
寒假总动员合肥工业大学出版社系列答案
寒假最佳学习方案寒假作业系列答案
相关题目
 (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….